[TS] CH03. 평활법 실습

Time Series
Author

김보람

Published

October 14, 2023

해당 자료는 전북대학교 이영미 교수님 2023고급시계열분석 자료임

패키지

install.packages("forecast")
Installing package into ‘/home/coco/R/x86_64-pc-linux-gnu-library/4.2’
(as ‘lib’ is unspecified)

Warning message in install.packages("forecast"):
“installation of package ‘forecast’ had non-zero exit status”
############## package
library(forecast) #ses
library(data.table)
library(ggplot2)
library(lmtest) #dwtest
library(TTR) #SMA
Registered S3 method overwritten by 'quantmod':
  method            from
  as.zoo.data.frame zoo 

Loading required package: zoo


Attaching package: ‘zoo’


The following objects are masked from ‘package:base’:

    as.Date, as.Date.numeric

자꾸 forecast 설치가 안되넹

options(repr.plot.width = 15, repr.plot.height = 8)

이동평균법

Kings data

kings=scan("http://robjhyndman.com/tsdldata/misc/kings.dat",skip=3)
kings
  1. 60
  2. 43
  3. 67
  4. 50
  5. 56
  6. 42
  7. 50
  8. 65
  9. 68
  10. 43
  11. 65
  12. 34
  13. 47
  14. 34
  15. 49
  16. 41
  17. 13
  18. 35
  19. 53
  20. 56
  21. 16
  22. 43
  23. 69
  24. 59
  25. 48
  26. 59
  27. 86
  28. 55
  29. 68
  30. 51
  31. 33
  32. 49
  33. 67
  34. 77
  35. 81
  36. 67
  37. 71
  38. 81
  39. 68
  40. 70
  41. 77
  42. 56
kingstimeseries = ts(kings)
plot(kingstimeseries, lwd=2)

kingstimeseries
A Time Series:
  1. 60
  2. 43
  3. 67
  4. 50
  5. 56
  6. 42
  7. 50
  8. 65
  9. 68
  10. 43
  11. 65
  12. 34
  13. 47
  14. 34
  15. 49
  16. 41
  17. 13
  18. 35
  19. 53
  20. 56
  21. 16
  22. 43
  23. 69
  24. 59
  25. 48
  26. 59
  27. 86
  28. 55
  29. 68
  30. 51
  31. 33
  32. 49
  33. 67
  34. 77
  35. 81
  36. 67
  37. 71
  38. 81
  39. 68
  40. 70
  41. 77
  42. 56
  • 1번왕은 60세까지, 2번왕은 43세까지, 3번왕은 67세까지…. 살았음
SMA(kings, n=3)
  1. <NA>
  2. <NA>
  3. 56.6666666666667
  4. 53.3333333333333
  5. 57.6666666666667
  6. 49.3333333333333
  7. 49.3333333333333
  8. 52.3333333333333
  9. 61
  10. 58.6666666666667
  11. 58.6666666666667
  12. 47.3333333333333
  13. 48.6666666666667
  14. 38.3333333333333
  15. 43.3333333333333
  16. 41.3333333333333
  17. 34.3333333333333
  18. 29.6666666666667
  19. 33.6666666666667
  20. 48
  21. 41.6666666666667
  22. 38.3333333333333
  23. 42.6666666666667
  24. 57
  25. 58.6666666666667
  26. 55.3333333333333
  27. 64.3333333333333
  28. 66.6666666666667
  29. 69.6666666666667
  30. 58
  31. 50.6666666666667
  32. 44.3333333333333
  33. 49.6666666666667
  34. 64.3333333333333
  35. 75
  36. 75
  37. 73
  38. 73
  39. 73.3333333333333
  40. 73
  41. 71.6666666666667
  42. 67.6666666666667

  • n=3이므로 첫번째, 두번째에서는 값을 알 수가 없다.

  • 56.6666666666667 = (60+43+67)/3

꼭 ts로 필수적으로 바꿀 필요는 없다.

class(SMA(kings, n=3))
'numeric' 
## window=3
kingstimeseriesSMA3 <- SMA(kingstimeseries,n=3)
plot.ts(kingstimeseries, lwd=2)
lines(kingstimeseriesSMA3, col='red', lty=2, lwd=2)
legend("topleft",
     legend=c("original", expression(m==3)), 
     col=c("black","red"),
     lty=c(1,2), lwd=2)

kingstimeseries
A Time Series:
  1. 60
  2. 43
  3. 67
  4. 50
  5. 56
  6. 42
  7. 50
  8. 65
  9. 68
  10. 43
  11. 65
  12. 34
  13. 47
  14. 34
  15. 49
  16. 41
  17. 13
  18. 35
  19. 53
  20. 56
  21. 16
  22. 43
  23. 69
  24. 59
  25. 48
  26. 59
  27. 86
  28. 55
  29. 68
  30. 51
  31. 33
  32. 49
  33. 67
  34. 77
  35. 81
  36. 67
  37. 71
  38. 81
  39. 68
  40. 70
  41. 77
  42. 56
kingstimeseriesSMA3
A Time Series:
  1. <NA>
  2. <NA>
  3. 56.6666666666667
  4. 53.3333333333333
  5. 57.6666666666667
  6. 49.3333333333333
  7. 49.3333333333333
  8. 52.3333333333333
  9. 61
  10. 58.6666666666667
  11. 58.6666666666667
  12. 47.3333333333333
  13. 48.6666666666667
  14. 38.3333333333333
  15. 43.3333333333333
  16. 41.3333333333333
  17. 34.3333333333333
  18. 29.6666666666667
  19. 33.6666666666667
  20. 48
  21. 41.6666666666667
  22. 38.3333333333333
  23. 42.6666666666667
  24. 57
  25. 58.6666666666667
  26. 55.3333333333333
  27. 64.3333333333333
  28. 66.6666666666667
  29. 69.6666666666667
  30. 58
  31. 50.6666666666667
  32. 44.3333333333333
  33. 49.6666666666667
  34. 64.3333333333333
  35. 75
  36. 75
  37. 73
  38. 73
  39. 73.3333333333333
  40. 73
  41. 71.6666666666667
  42. 67.6666666666667
## window=3 vs. 10
plot.ts(kingstimeseries, lwd=2)
lines(kingstimeseriesSMA3, col='red', lty=2, lwd=2)
lines( SMA(kingstimeseries,n=10), col='blue', lty=2, lwd=2)
legend("topleft",
 legend=c("original", expression(m==3), expression(m==10)),
 col=c("black","red","blue"),
 lty=c(1,2,2), lwd=2)

모형 평가

length(kings)
42 
## m=3
mean((kings[-1]- kingstimeseriesSMA3[-42])^2, na.rm=T) ##MSE : e_t(1)= z_{t+1} - hat z_t, t=3,4,...
mean(abs(kings[-1]- kingstimeseriesSMA3[-42]), na.rm=T) ##MAE
mean(abs(kings[-1]- kingstimeseriesSMA3[-42])/kings[-1], na.rm=T)*100 ##MAPE
262.606837606838
12.8119658119658
31.5545022415299

na.rm=T : 결측치는 제외하고

## m=10
mean((kings[-1]- SMA(kingstimeseries,n=10)[-42])^2, na.rm=T) ##MSE
mean(abs(kings[-1]- SMA(kingstimeseries,n=10)[-42]), na.rm=T) ##MAE
mean(abs(kings[-1]- SMA(kingstimeseries,n=10)[-42])/kings[-1], na.rm=T)*100 ##MAPE
288.6253125
13.996875
35.7375097004325 
## m=4
mean((kings[-1]- SMA(kingstimeseries,n=4)[-42])^2, na.rm=T) ##MSE
mean(abs(kings[-1]- SMA(kingstimeseries,n=4)[-42]), na.rm=T) ##MAE
mean(abs(kings[-1]- SMA(kingstimeseries,n=4)[-42])/kings[-1], na.rm=T)*100 ##MAPE
239.009868421053
12.1315789473684
29.8129038055302
  • MSE가 제일 작은 값 찾아줘야 함

mindex data

z <- scan("mindex.txt")
mindex <- ts(z, start = c(1986, 1), frequency = 12)
mindex
A Time Series: 9 × 12
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1986 9.3 10.7 13.3 14.1 17.8 18.1 19.4 18.8 19.1 18.4 18.0 17.0
1987 19.5 20.1 19.4 15.7 15.6 16.1 14.9 16.0 14.6 18.3 18.2 23.0
1988 22.2 22.1 18.8 17.7 13.8 12.7 16.5 15.6 16.3 10.7 10.4 7.0
1989 4.7 4.5 4.0 6.0 6.2 5.7 4.4 4.2 5.0 5.8 6.4 4.9
1990 7.9 8.2 11.8 10.0 11.1 11.7 12.4 15.2 14.0 15.2 12.9 18.0
1991 14.4 12.7 8.3 11.5 11.9 11.6 10.3 8.5 11.6 12.3 14.5 11.1
1992 11.8 12.4 12.7 9.8 10.0 10.2 9.6 6.9 5.3 4.8 4.6 1.9
1993 3.8 4.7 7.7 7.0 7.2 7.8 8.6 11.4 10.7 11.8 11.3 16.0
1994 13.2 12.0 8.5 11.4 
mindex_sma3 <- SMA(mindex,n=3)
mindex_sma10 <- SMA(mindex,n=10)
plot.ts(mindex, lwd=2)
lines(mindex_sma3, col='red', lty=2, lwd=2)
lines(mindex_sma10, col='blue', lty=2, lwd=2)
legend("topright",
     legend=c("original", expression(m==3), expression(m==10)),
     col=c("black","red","blue"),
     lty=c(1,2,2), lwd=2)

depart data

z <- scan("depart.txt")
mindex <- ts(z, start = c(1986, 1), frequency = 12)
mindex
A Time Series: 5 × 12
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1986 423 458 607 564 536 536 804 540 488 627 672 1447
1987 514 518 699 654 612 612 884 605 547 705 698 1555
1988 561 564 773 717 665 667 994 661 616 786 806 1754
1989 622 636 874 831 769 779 1142 764 718 930 943 2039
1990 736 752 1057 947 868 931 1311 896 867 1073 1069 2333 
mindex_sma3 <- SMA(mindex,n=3)
mindex_sma12 <- SMA(mindex,n=12)
plot.ts(mindex, lwd=2)
lines(mindex_sma3, col='red', lty=2, lwd=2)
lines(mindex_sma12, col='blue', lty=2, lwd=2)
legend("topright",
     legend=c("original", expression(m==3), expression(m==12)),
     col=c("black","red","blue"),
     lty=c(1,2,2), lwd=2)

  • 계절 성분 데이터를 평활하면.. m에 따라서 계절 성분이 없어진당
plot.ts(mindex-mindex_sma12)

  • 계절성분만 있다. 이분산성이 조금 보이긴 하지만. 추후에 ch4장에서 분해법 할 때

단순지수평활법

z <- scan("mindex.txt")
mindex <- ts(z, start = c(1986, 1), frequency = 12)
tmp.dat <- data.frame(day = seq.Date(as.Date("1986-01-01"),
 by='month',
 length.out=length(z)), 
              ind = z)
head(tmp.dat)
A data.frame: 6 × 2
day ind
<date> <dbl>
1 1986-01-01 9.3
2 1986-02-01 10.7
3 1986-03-01 13.3
4 1986-04-01 14.1
5 1986-05-01 17.8
6 1986-06-01 18.1 
ggplot(tmp.dat, aes(day, ind))+geom_line(col='skyblue', lwd=2) +
 geom_point(col='steelblue', cex=2)+
 ggtitle("중간재 출하지수")+
 theme_bw()+
 theme(plot.title = element_text(size=30),
 axis.title = element_blank())

plot(mindex)

  • 추세도 없어보이고 계절성분도 없어보이네? -> 단순지수평활을 하자

단순지수평활 \(\alpha=0.3\)

- 평활상수

  • alpha: level

  • beta: 기울기

  • gamma: 계절

- 평활 초기값

  • 아래 내용 살펴보자

  • 단순지수평활에서는 초기값을 x[1]값 을 사용함

?HoltWinters
HoltWinters {stats} R Documentation

Holt-Winters Filtering

Description

Computes Holt-Winters Filtering of a given time series. Unknown parameters are determined by minimizing the squared prediction error.

Usage

HoltWinters(x, alpha = NULL, beta = NULL, gamma = NULL,
            seasonal = c("additive", "multiplicative"),
            start.periods = 2, l.start = NULL, b.start = NULL,
            s.start = NULL,
            optim.start = c(alpha = 0.3, beta = 0.1, gamma = 0.1),
            optim.control = list())

Arguments

x

An object of class ts
alpha

alpha parameter of Holt-Winters Filter.
beta

beta parameter of Holt-Winters Filter. If set to FALSE, the function will do exponential smoothing.
gamma

gamma parameter used for the seasonal component. If set to FALSE, an non-seasonal model is fitted.
seasonal

Character string to select an "additive" (the default) or "multiplicative" seasonal model. The first few characters are sufficient. (Only takes effect if gamma is non-zero).
start.periods

Start periods used in the autodetection of start values. Must be at least 2.
l.start

Start value for level (a[0]).
b.start

Start value for trend (b[0]).
s.start

Vector of start values for the seasonal component (s_1[0] \ldots s_p[0])
optim.start

Vector with named components alpha, beta, and gamma containing the starting values for the optimizer. Only the values needed must be specified. Ignored in the one-parameter case.
optim.control

Optional list with additional control parameters passed to optim if this is used. Ignored in the one-parameter case.

Details

The additive Holt-Winters prediction function (for time series with period length p) is

\hat Y[t+h] = a[t] + h b[t] + s[t - p + 1 + (h - 1) \bmod p],

where a[t], b[t] and s[t] are given by

a[t] = \alpha (Y[t] - s[t-p]) + (1-\alpha) (a[t-1] + b[t-1])

b[t] = \beta (a[t] -a[t-1]) + (1-\beta) b[t-1]

s[t] = \gamma (Y[t] - a[t]) + (1-\gamma) s[t-p]

The multiplicative Holt-Winters prediction function (for time series with period length p) is

\hat Y[t+h] = (a[t] + h b[t]) \times s[t - p + 1 + (h - 1) \bmod p].

where a[t], b[t] and s[t] are given by

a[t] = \alpha (Y[t] / s[t-p]) + (1-\alpha) (a[t-1] + b[t-1])

b[t] = \beta (a[t] - a[t-1]) + (1-\beta) b[t-1]

s[t] = \gamma (Y[t] / a[t]) + (1-\gamma) s[t-p]

The data in x are required to be non-zero for a multiplicative model, but it makes most sense if they are all positive.

The function tries to find the optimal values of \alpha and/or \beta and/or \gamma by minimizing the squared one-step prediction error if they are NULL (the default). optimize will be used for the single-parameter case, and optim otherwise.

For seasonal models, start values for a, b and s are inferred by performing a simple decomposition in trend and seasonal component using moving averages (see function decompose) on the start.periods first periods (a simple linear regression on the trend component is used for starting level and trend). For level/trend-models (no seasonal component), start values for a and b are x[2] and x[2] - x[1], respectively. For level-only models (ordinary exponential smoothing), the start value for a is x[1].

Value

An object of class "HoltWinters", a list with components:

fitted

A multiple time series with one column for the filtered series as well as for the level, trend and seasonal components, estimated contemporaneously (that is at time t and not at the end of the series).
x

The original series
alpha

alpha used for filtering
beta

beta used for filtering
gamma

gamma used for filtering
coefficients

A vector with named components a, b, s1, ..., sp containing the estimated values for the level, trend and seasonal components
seasonal

The specified seasonal parameter
SSE

The final sum of squared errors achieved in optimizing
call

The call used

Author(s)

David Meyer David.Meyer@wu.ac.at

References

C. C. Holt (1957) Forecasting seasonals and trends by exponentially weighted moving averages, ONR Research Memorandum, Carnegie Institute of Technology 52. (reprint at doi:10.1016/j.ijforecast.2003.09.015).

P. R. Winters (1960). Forecasting sales by exponentially weighted moving averages. Management Science, 6, 324–342. doi:10.1287/mnsc.6.3.324.

See Also

predict.HoltWinters, optim.

Examples


require(graphics)

## Seasonal Holt-Winters
(m <- HoltWinters(co2))
plot(m)
plot(fitted(m))

(m <- HoltWinters(AirPassengers, seasonal = "mult"))
plot(m)

## Non-Seasonal Holt-Winters
x <- uspop + rnorm(uspop, sd = 5)
m <- HoltWinters(x, gamma = FALSE)
plot(m)

## Exponential Smoothing
m2 <- HoltWinters(x, gamma = FALSE, beta = FALSE)
lines(fitted(m2)[,1], col = 3)
[Package stats version 4.2.2 ]
fit0 <- HoltWinters(mindex,
                    alpha=0.3,
                    beta=FALSE,
                    gamma=FALSE)
fit0
Holt-Winters exponential smoothing without trend and without seasonal component.

Call:
HoltWinters(x = mindex, alpha = 0.3, beta = FALSE, gamma = FALSE)

Smoothing parameters:
 alpha: 0.3
 beta : FALSE
 gamma: FALSE

Coefficients:
     [,1]
a 11.2236

\[S_n^{(1)} = w Z_n + (1-w) S_{n-1}^{(1)}\]

tail(fit0$fitted)
A Time Series: 6 × 2
xhat level
Nov 1993 9.97951 9.97951
Dec 1993 10.37566 10.37566
Jan 1994 12.06296 12.06296
Feb 1994 12.40407 12.40407
Mar 1994 12.28285 12.28285
Apr 1994 11.14800 11.14800

coefficients: 11.14800 마지막 평활값

ls(fit0)
  1. 'alpha'
  2. 'beta'
  3. 'call'
  4. 'coefficients'
  5. 'fitted'
  6. 'gamma'
  7. 'seasonal'
  8. 'SSE'
  9. 'x'
head(fit0$fitted)   ## 평활값
A Time Series: 6 × 2
xhat level
Feb 1986 9.30000 9.30000
Mar 1986 9.72000 9.72000
Apr 1986 10.79400 10.79400
May 1986 11.78580 11.78580
Jun 1986 13.59006 13.59006
Jul 1986 14.94304 14.94304 
head(cbind(fit0$fitted, mindex))
A Time Series: 6 × 3
fit0$fitted.xhat fit0$fitted.level mindex
Jan 1986 NA NA 9.3
Feb 1986 9.30000 9.30000 10.7
Mar 1986 9.72000 9.72000 13.3
Apr 1986 10.79400 10.79400 14.1
May 1986 11.78580 11.78580 17.8
Jun 1986 13.59006 13.59006 18.1

\[S_n^{(1)} = w \sum_{j=0}^{n-1} (1-w)^j Z_{n-j} + (1-w)^n S_0^{(1)}\]

\(S_2^{(1)} = w Z_2 + (1-w) S_0^{(1)}\)

0.3*10.7 + 0.7*9.3
9.72

\(S_3^{(1)} = w Z_3 + w (1-w) Z_2 + (1-w)^2 S_0^{(1)}\)

0.3*13.3 + 0.3*0.7*10.7 + 0.7*0.7*9.3
10.794 
fit0$SSE
792.968599702168 
plot(fit0, lwd=3, cex.main = 2)
legend("topright", legend=c("observed", "ses"), lty=1,lwd=c(1,3), col=1:2)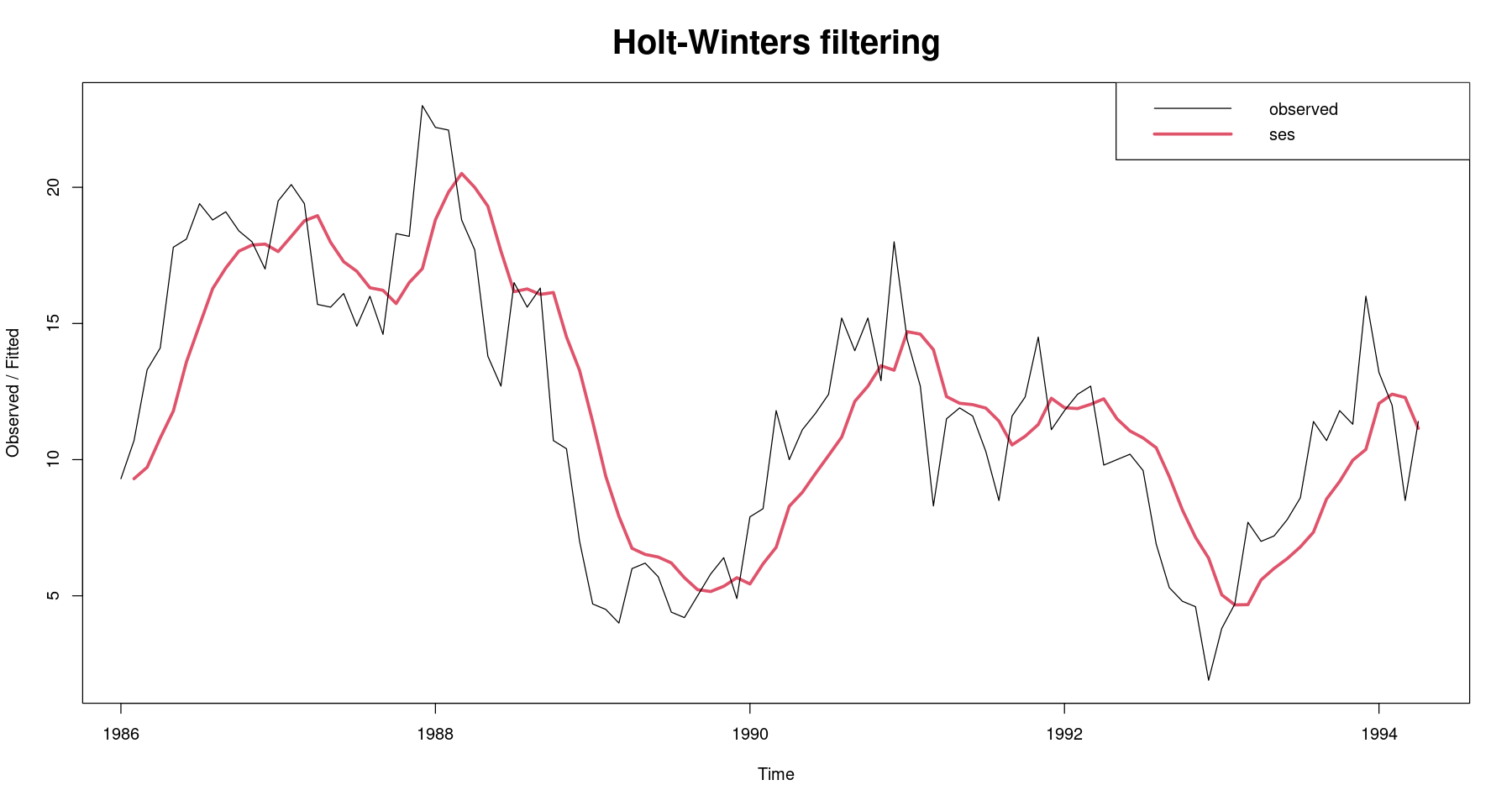

fit01 <- ses(mindex,
 alpha = 0.3,
 initial = 'simple',
 h = 10) ##Exponential smoothing forecasts
fit01
         Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
May 1994        11.2236 7.614786 14.83241 5.704397 16.74280
Jun 1994        11.2236 7.455888 14.99131 5.461383 16.98581
Jul 1994        11.2236 7.303425 15.14377 5.228212 17.21898
Aug 1994        11.2236 7.156674 15.29052 5.003775 17.44342
Sep 1994        11.2236 7.015037 15.43216 4.787159 17.66003
Oct 1994        11.2236 6.878013 15.56918 4.577601 17.86959
Nov 1994        11.2236 6.745181 15.70201 4.374450 18.07274
Dec 1994        11.2236 6.616176 15.83102 4.177155 18.27004
Jan 1995        11.2236 6.490686 15.95651 3.985235 18.46196
Feb 1995        11.2236 6.368439 16.07875 3.798273 18.64892
ls(fit01)
  1. 'fitted'
  2. 'level'
  3. 'lower'
  4. 'mean'
  5. 'method'
  6. 'model'
  7. 'residuals'
  8. 'series'
  9. 'upper'
  10. 'x'
summary(fit01)

Forecast method: Simple exponential smoothing

Model Information:
Simple exponential smoothing 

Call:
 ses(y = mindex, h = 10, initial = "simple", alpha = 0.3) 

  Smoothing parameters:
    alpha = 0.3 

  Initial states:
    l = 9.3 

  sigma:  2.816
Error measures:
                     ME    RMSE      MAE       MPE     MAPE      MASE      ACF1
Training set 0.06411989 2.81597 2.248923 -7.657492 24.93904 0.4105067 0.6648489

Forecasts:
         Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
May 1994        11.2236 7.614786 14.83241 5.704397 16.74280
Jun 1994        11.2236 7.455888 14.99131 5.461383 16.98581
Jul 1994        11.2236 7.303425 15.14377 5.228212 17.21898
Aug 1994        11.2236 7.156674 15.29052 5.003775 17.44342
Sep 1994        11.2236 7.015037 15.43216 4.787159 17.66003
Oct 1994        11.2236 6.878013 15.56918 4.577601 17.86959
Nov 1994        11.2236 6.745181 15.70201 4.374450 18.07274
Dec 1994        11.2236 6.616176 15.83102 4.177155 18.27004
Jan 1995        11.2236 6.490686 15.95651 3.985235 18.46196
Feb 1995        11.2236 6.368439 16.07875 3.798273 18.64892
tail(cbind(fit0$fitted, mindex))
A Time Series: 6 × 3
fit0$fitted.xhat fit0$fitted.level mindex
Nov 1993 9.97951 9.97951 11.3
Dec 1993 10.37566 10.37566 16.0
Jan 1994 12.06296 12.06296 13.2
Feb 1994 12.40407 12.40407 12.0
Mar 1994 12.28285 12.28285 8.5
Apr 1994 11.14800 11.14800 11.4

- 예측 갱신

\[S_n^{(1)} = wZ_n + (1-w)S_{n-1}^{(1)}\]

\(S_{100}^{(1)} = w Z_{100} + (1-w) S_{(99)}^{(1)}\)

0.3*11.4+0.7*11.14800
11.2236 
0.3*11.4+0.7*11.147995
11.2235965 
summary(fit01)

Forecast method: Simple exponential smoothing

Model Information:
Simple exponential smoothing 

Call:
 ses(y = mindex, h = 10, initial = "simple", alpha = 0.3) 

  Smoothing parameters:
    alpha = 0.3 

  Initial states:
    l = 9.3 

  sigma:  2.816
Error measures:
                     ME    RMSE      MAE       MPE     MAPE      MASE      ACF1
Training set 0.06411989 2.81597 2.248923 -7.657492 24.93904 0.4105067 0.6648489

Forecasts:
         Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
May 1994        11.2236 7.614786 14.83241 5.704397 16.74280
Jun 1994        11.2236 7.455888 14.99131 5.461383 16.98581
Jul 1994        11.2236 7.303425 15.14377 5.228212 17.21898
Aug 1994        11.2236 7.156674 15.29052 5.003775 17.44342
Sep 1994        11.2236 7.015037 15.43216 4.787159 17.66003
Oct 1994        11.2236 6.878013 15.56918 4.577601 17.86959
Nov 1994        11.2236 6.745181 15.70201 4.374450 18.07274
Dec 1994        11.2236 6.616176 15.83102 4.177155 18.27004
Jan 1995        11.2236 6.490686 15.95651 3.985235 18.46196
Feb 1995        11.2236 6.368439 16.07875 3.798273 18.64892
plot(fit01,, cex.main = 2)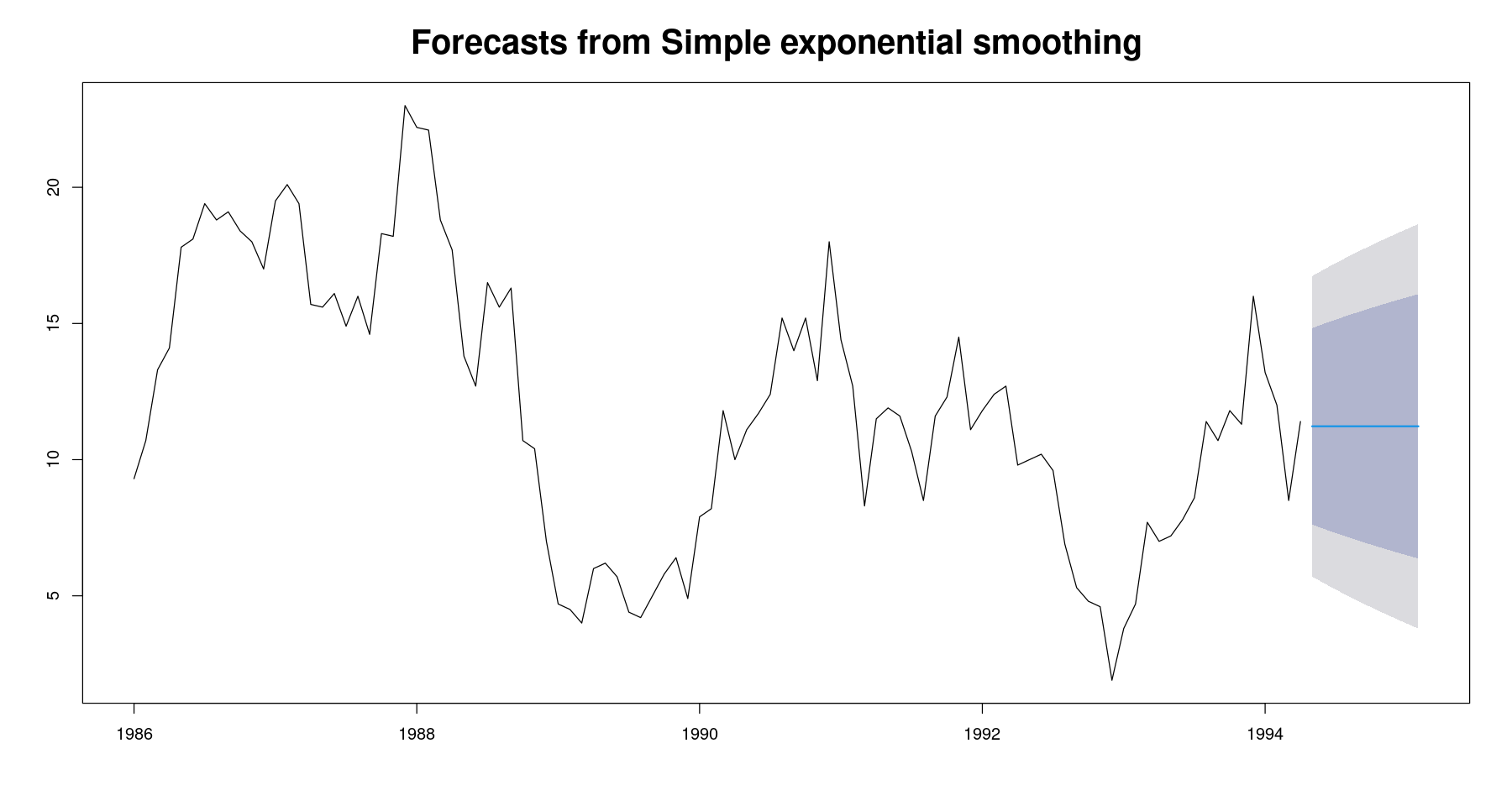

여러 평활상수에 따른 변화

w <-c(seq(0.1,0.8,0.1), seq(0.81, 0.99, 0.01))
SSE_ses <- sapply(w, function(alpha) HoltWinters(mindex,
                 alpha=alpha,
                 beta=FALSE,
                 gamma=FALSE)$SSE)
plot(w,SSE_ses, type="o", xlab="weight", ylab="SSE", pch=16,
     main="1 시차 후 예측오차의 제곱합",
     cex.main = 2, cex.lab=2)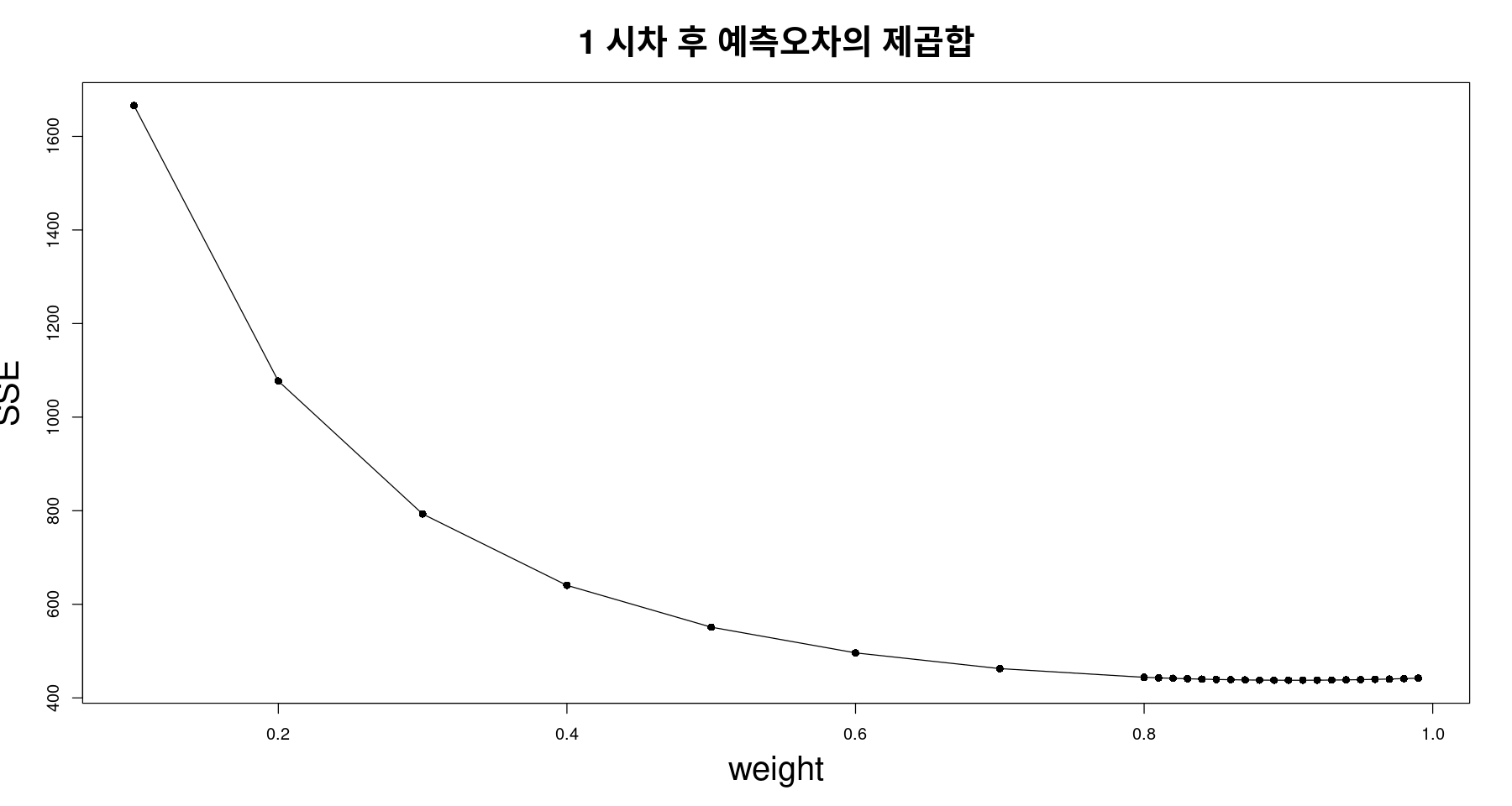

- SSE를 가장 작게 하는 값 찾자

which.min(SSE_ses)
18 
w[which.min(SSE_ses)]
0.9 
plot(w[-(1:7)],SSE_ses[-(1:7)], type="o", xlab="weight", ylab="SSE", pch=16,
 main="1 시차 후 예측오차의 제곱합",
 cex.main = 2, cex.lab=2)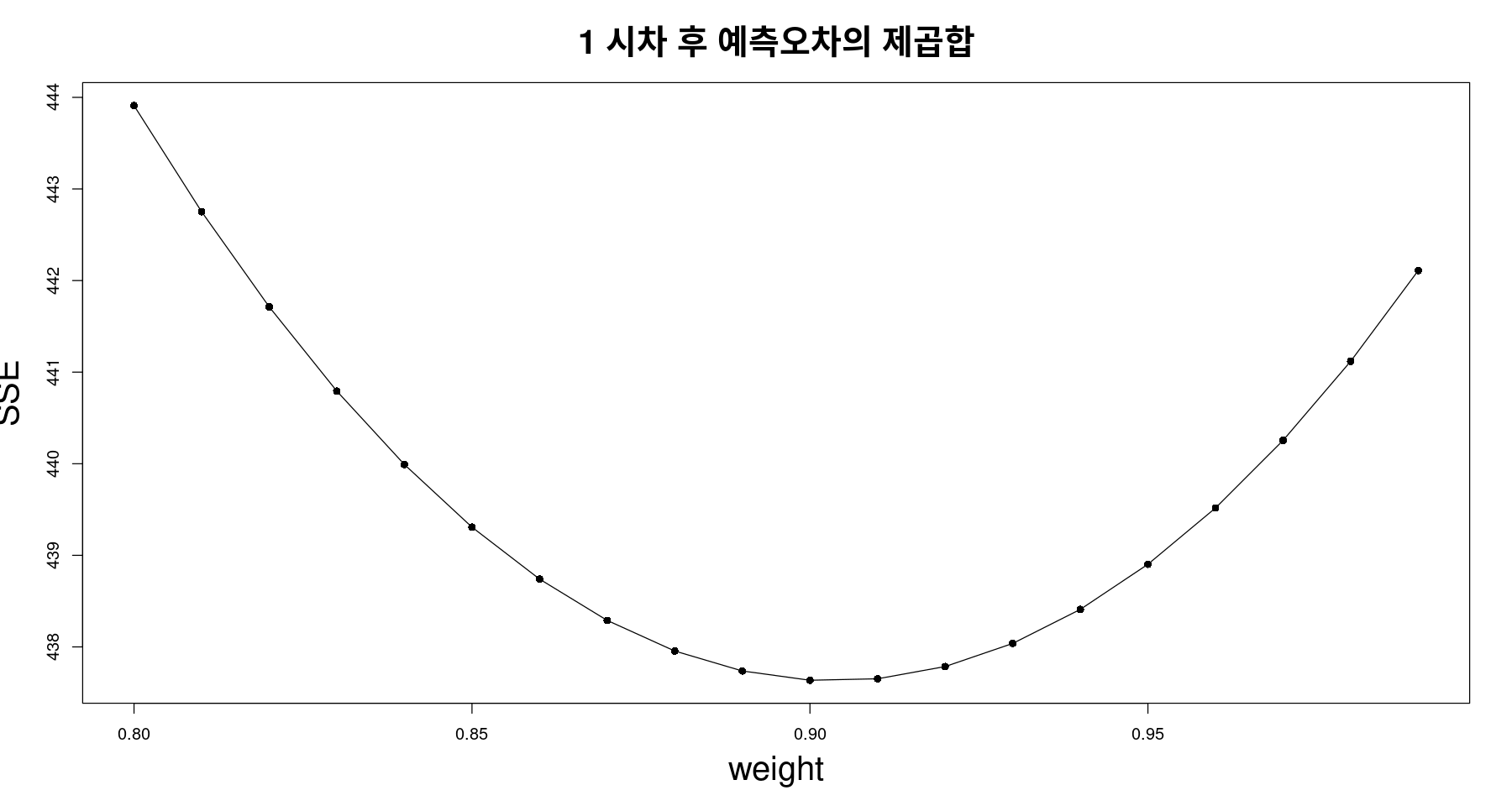

fit1 <- ses(mindex, alpha=w[which.min(SSE_ses)], initial = "simple", h=6)
plot(fit1, xlab="", ylab="",
 main="중간재 출하지수와 단순지수평활값 alpha=0.9",
 lty=1,col="black",
 cex.main = 2, cex.lab=2 )
lines(fitted(fit1), col="red", lty=2)
legend("topright", legend=c("Mindex", expression(alpha==0.9)),
 lty=1:2,col=c("black","red"))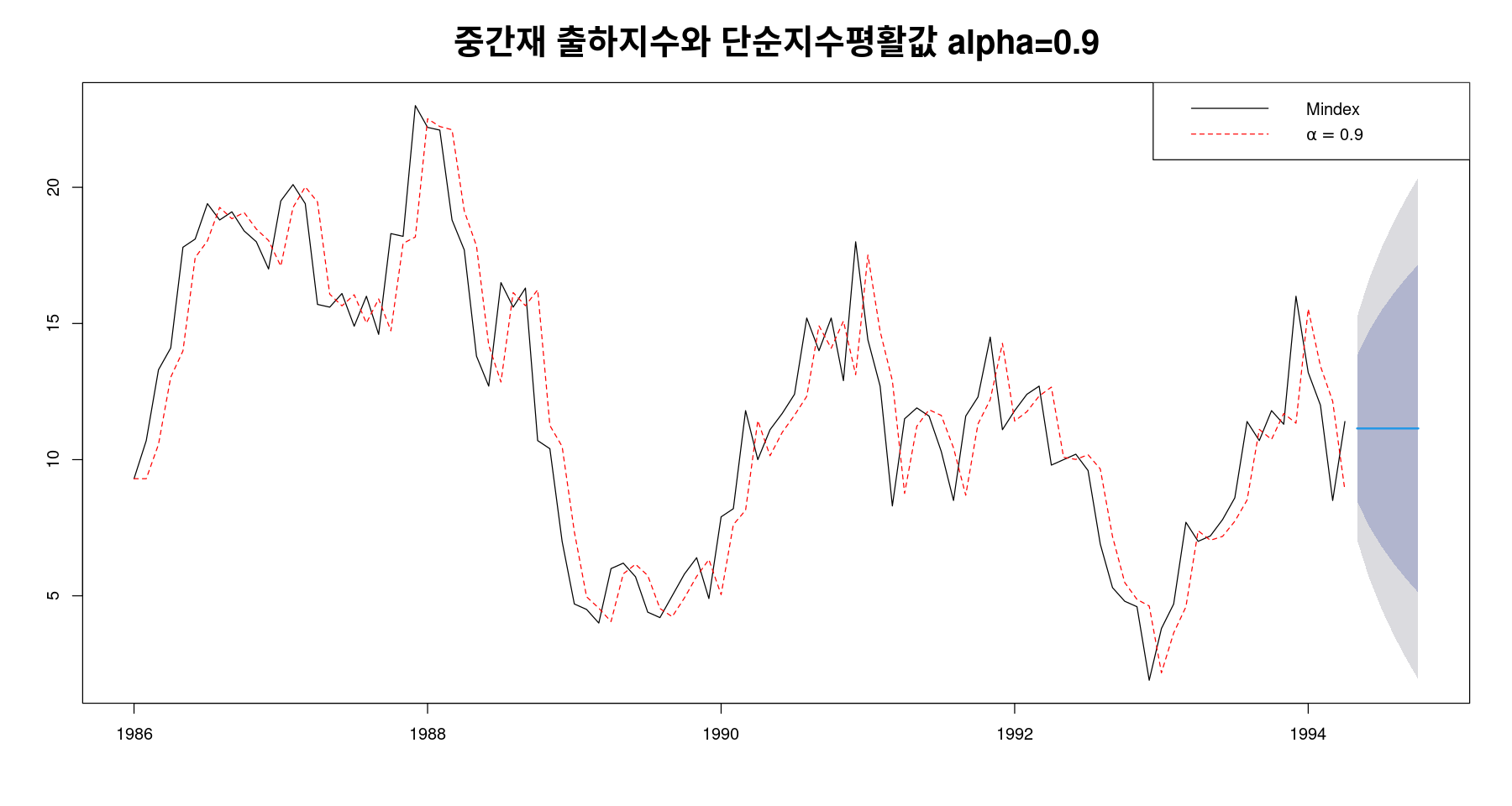

fit0_w <- HoltWinters(mindex,
 beta=FALSE,
 gamma=FALSE)
fit0_w
Holt-Winters exponential smoothing without trend and without seasonal component.

Call:
HoltWinters(x = mindex, beta = FALSE, gamma = FALSE)

Smoothing parameters:
 alpha: 0.9036403
 beta : FALSE
 gamma: FALSE

Coefficients:
      [,1]
a 11.15433

잔차

fit1 <- ses(mindex, alpha=fit0_w$alpha, h=12)
ls(fit1)
  1. 'fitted'
  2. 'level'
  3. 'lower'
  4. 'mean'
  5. 'method'
  6. 'model'
  7. 'residuals'
  8. 'series'
  9. 'upper'
  10. 'x'
plot(fit1$residuals, ylab="residual",
 main="예측 오차의 시계열그림 : alpha=0.9",
 cex.main = 2, cex.lab=2); abline(h=0)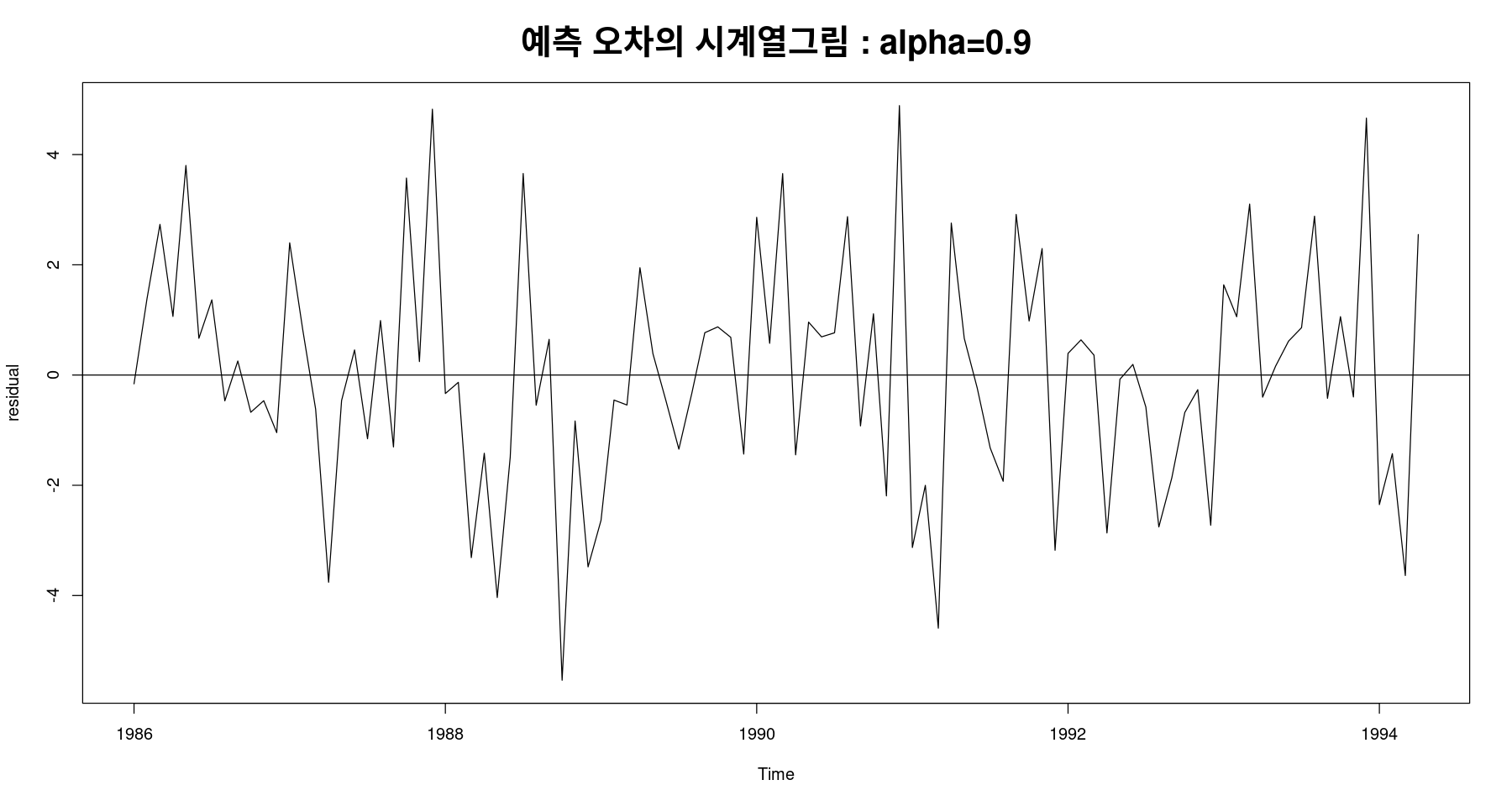

오차의 평균이 0인가?

t.test(fit1$residual)

    One Sample t-test

data:  fit1$residual
t = 0.089225, df = 99, p-value = 0.9291
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -0.3983934  0.4359099
sample estimates:
 mean of x 
0.01875828

오차가 독립인가?

dwtest(lm(fit1$residual~1))

    Durbin-Watson test

data:  lm(fit1$residual ~ 1)
DW = 2.0244, p-value = 0.549
alternative hypothesis: true autocorrelation is greater than 0
dwtest(lm(fit1$residual~1), alternative = "two.sided")

    Durbin-Watson test

data:  lm(fit1$residual ~ 1)
DW = 2.0244, p-value = 0.902
alternative hypothesis: true autocorrelation is not 0
fit2 <- ses(mindex, alpha=0.3, h=6)
plot(fit2, xlab="year", ylab="mindex",
 main=expression("중간재 출하지수와 단순지수평활값 "~alpha==0.3),
 lty=1,col="black",
 cex.main = 2,
 cex.lab=2)
lines(fitted(fit2), col="red", lty=2)
legend("topright",
 legend=c("Mindex",expression(alpha==0.3)),
 lty=1:2,
 col=c("black","red"))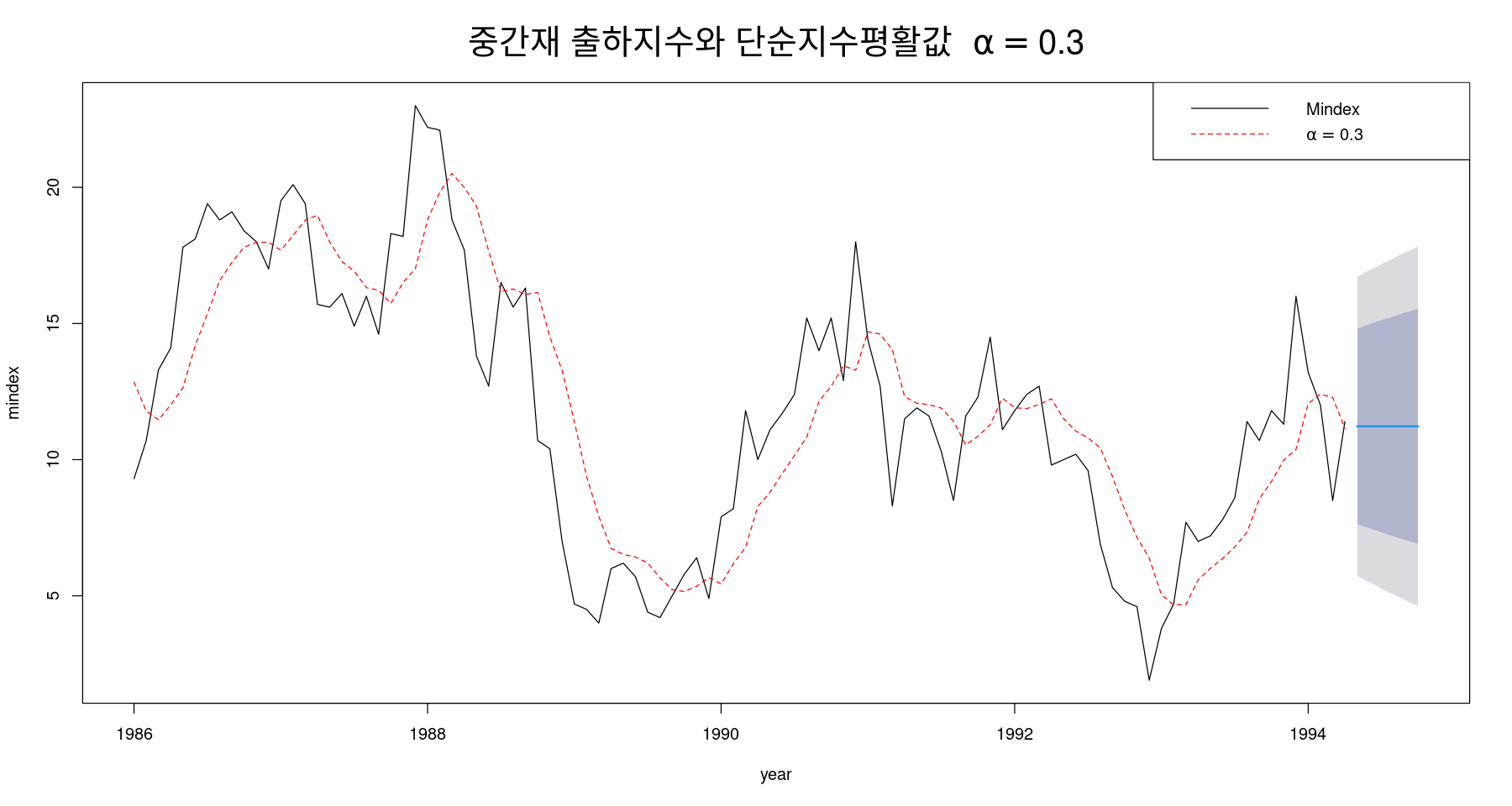

plot(fit2$residuals, ylab="residual",
 main=expression("중간재 출하지수와 단순지수평활값 "~alpha==0.3),
 cex.main = 2,
 cex.lab=2); abline(h=0)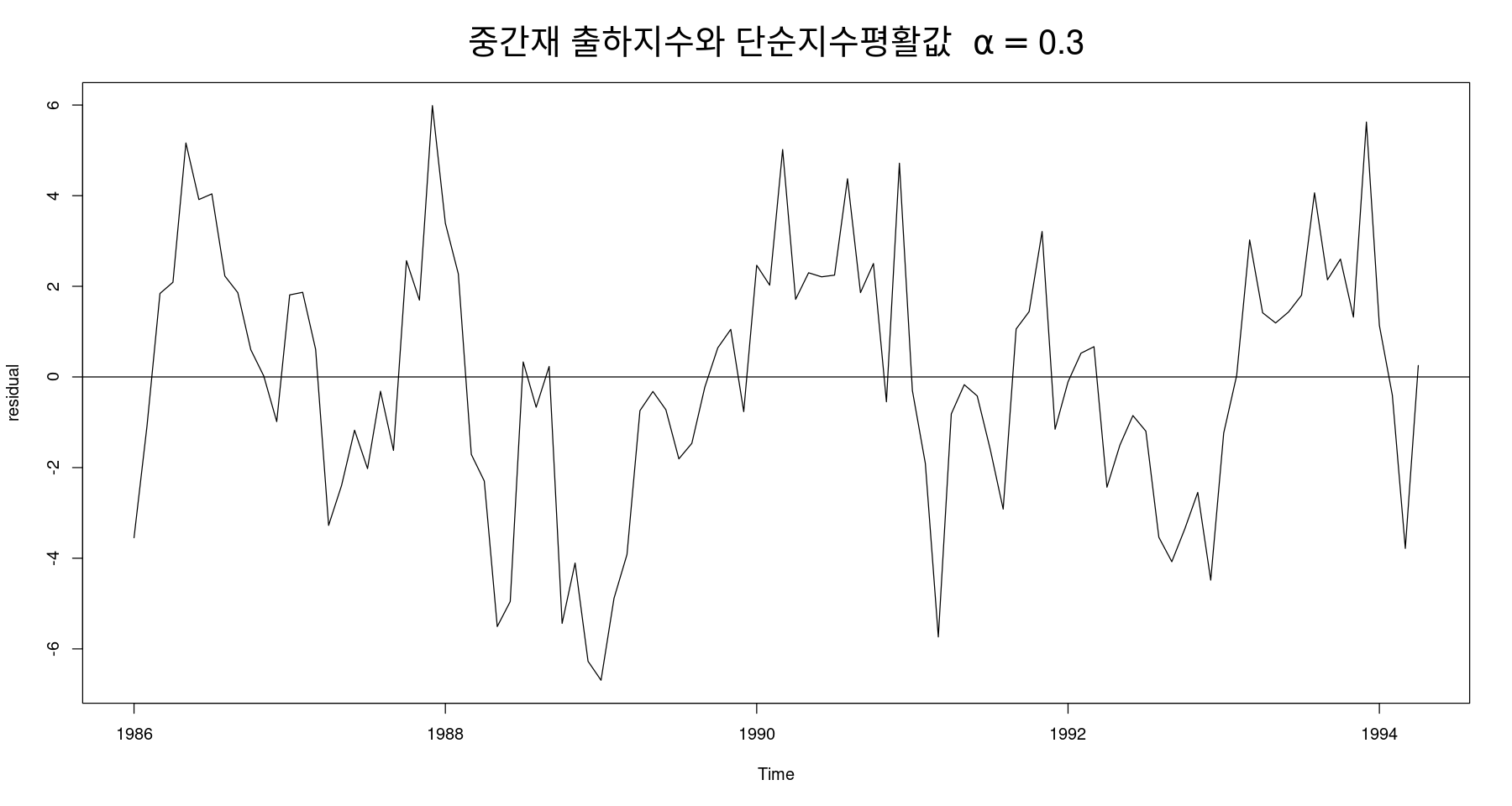

오차의 평균이 0인가?

t.test(fit2$residual)

    One Sample t-test

data:  fit2$residual
t = -0.19433, df = 99, p-value = 0.8463
alternative hypothesis: true mean is not equal to 0
95 percent confidence interval:
 -0.6067721  0.4985236
sample estimates:
  mean of x 
-0.05412425

오차가 독립인가?

dwtest(lm(fit2$residual~1))

    Durbin-Watson test

data:  lm(fit2$residual ~ 1)
DW = 0.70285, p-value = 2.853e-11
alternative hypothesis: true autocorrelation is greater than 0

이중지수평활법

z <- scan("stock.txt")
stock <- ts(z, start=c(1984,1), frequency=12)
plot(stock, main = '월별주가지수', cex.main=2, cex.lab=2)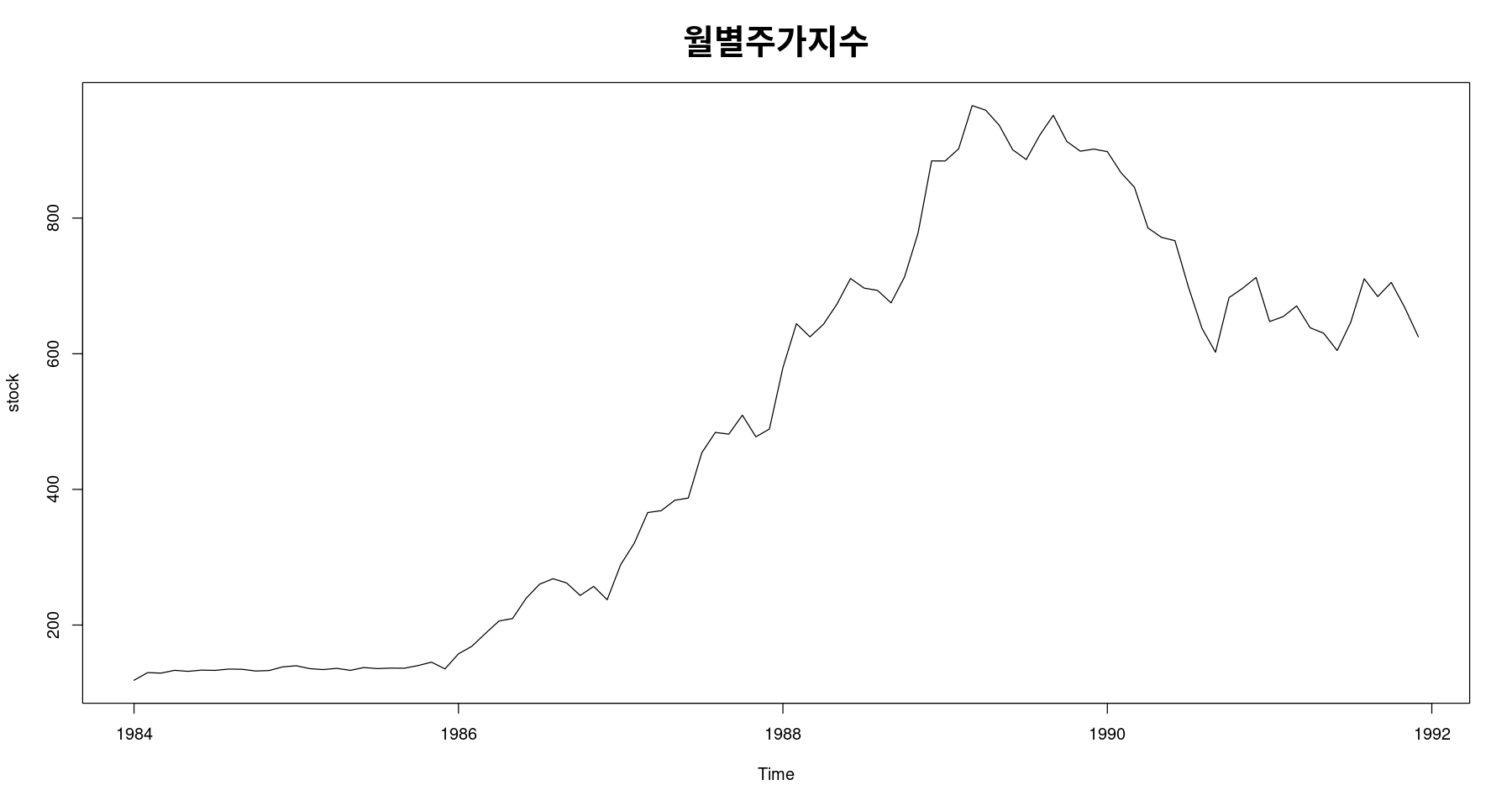

1모수 이중지수평활 \((\alpha = \beta)\)

fit4 = holt(stock, alpha=0.6, beta=0.6, h=6)
fit4$model
Holt's method 

Call:
 holt(y = stock, h = 6, alpha = 0.6, beta = 0.6) 

  Smoothing parameters:
    alpha = 0.6 
    beta  = 0.6 

  Initial states:
    l = 115.6009 
    b = 6.8098 

  sigma:  40.2546

     AIC     AICc      BIC 
1149.575 1149.836 1157.268 
plot(fit4, ylab="", xlab="", lty=1, col="black",
 main="주가지수와 이중지수평활값 : alpha=beta=0.6"
 )
lines(fitted(fit4), col="red", lty=2)
legend("topleft", lty=1:2, col=c("black","red"), c("Index", "Double"), bty = "n")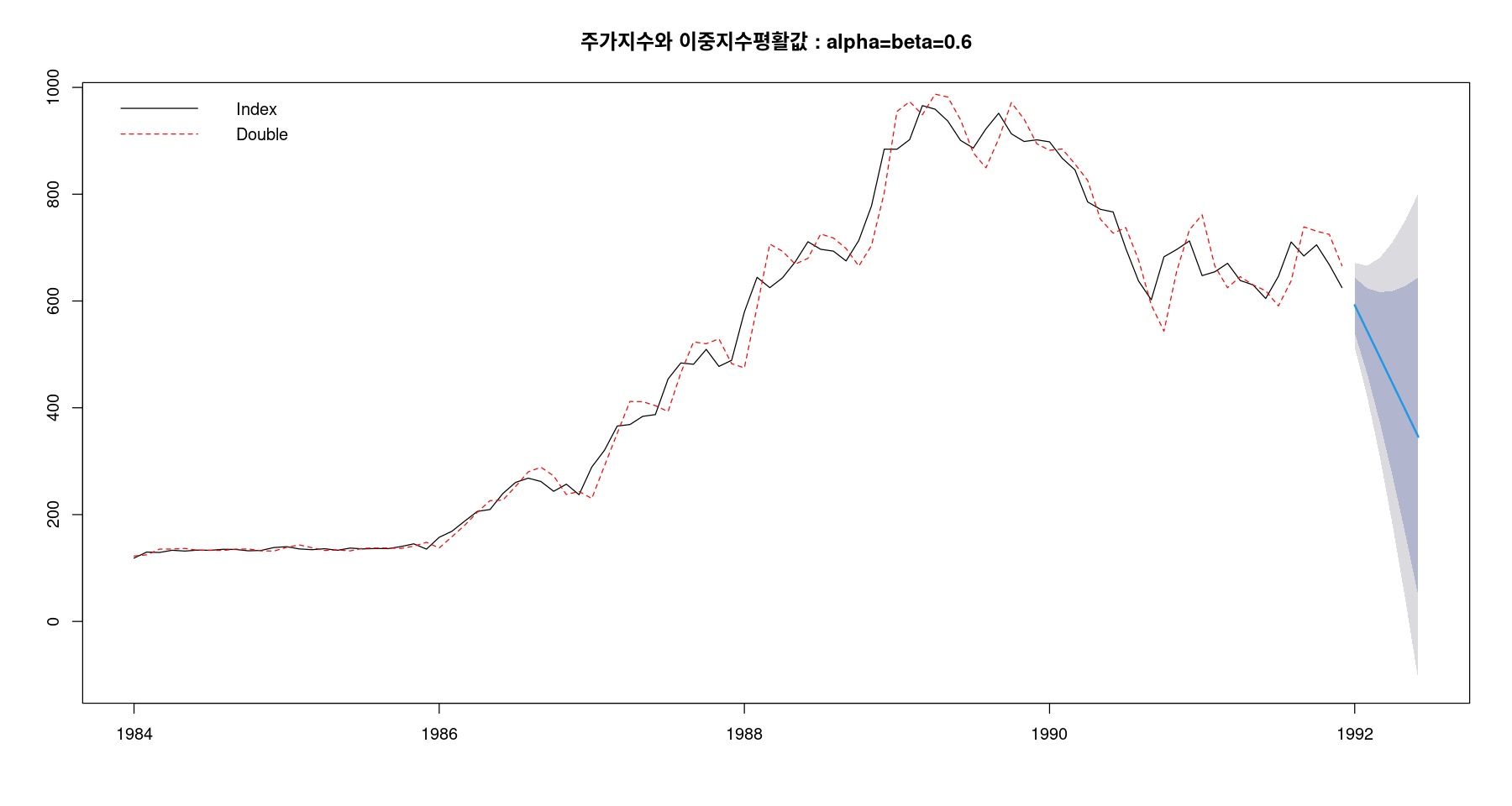

이중지수평활 \(\alpha, \beta\) 추정

fit5 = holt(stock, h=6)
fit5$model
Holt's method 

Call:
 holt(y = stock, h = 6) 

  Smoothing parameters:
    alpha = 0.9999 
    beta  = 0.1071 

  Initial states:
    l = 124.1137 
    b = 3.4954 

  sigma:  31.8609

     AIC     AICc      BIC 
1108.677 1109.343 1121.498 
fit50 <- HoltWinters(stock,
                     gamma = FALSE)
fit50
Holt-Winters exponential smoothing with trend and without seasonal component.

Call:
HoltWinters(x = stock, gamma = FALSE)

Smoothing parameters:
 alpha: 1
 beta : 0.1094451
 gamma: FALSE

Coefficients:
        [,1]
a 625.060000
b  -7.097122
predict(fit50, n.ahead=12, prediction.interval = T, level=0.95)
A Time Series: 12 × 3
fit upr lwr
Jan 1992 617.9629 680.0626 555.8631
Feb 1992 610.8658 703.6185 518.1130
Mar 1992 603.7686 723.4869 484.0504
Apr 1992 596.6715 742.0570 451.2860
May 1992 589.5744 760.1877 418.9611
Jun 1992 582.4773 778.2851 386.6695
Jul 1992 575.3801 796.5695 354.1907
Aug 1992 568.2830 815.1705 321.3955
Sep 1992 561.1859 834.1678 288.2040
Oct 1992 554.0888 853.6121 254.5655
Nov 1992 546.9917 873.5358 220.4475
Dec 1992 539.8945 893.9596 185.8294 
fit5
         Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
Jan 1992       618.0360 577.2045 658.8674 555.5897 680.4822
Feb 1992       611.0079 550.0961 671.9196 517.8514 704.1644
Mar 1992       603.9798 525.4452 682.5144 483.8715 724.0881
Apr 1992       596.9517 501.6745 692.2290 451.2377 742.6657
May 1992       589.9237 478.2155 701.6319 419.0807 760.7666
Jun 1992       582.8956 454.7987 710.9924 386.9883 778.8028

- 시점 n에서 l-시차 후의 예측값

\[\hat {Z}_n(l) = \hat {\beta}_{0,n} + \hat {\beta}_{1,n}(n+l) = \left( 2+ \dfrac{w}{1-w}l \right) S_n^{(1)} - \left( 1+ \dfrac{w}{1-w}l \right) S_n^{(2)}\]

plot(fit5, ylab="Index", xlab="year", lty=1, col="black",
 main=expression("중간재 출하지수와 이중지수평활값 : "~alpha~","~beta~ " : estimated"),
 cex.main=2)
lines(fitted(fit5), col="red", lty=2)
legend("topleft", lty=1:2, col=c("black","red"), c("Index", "Double"))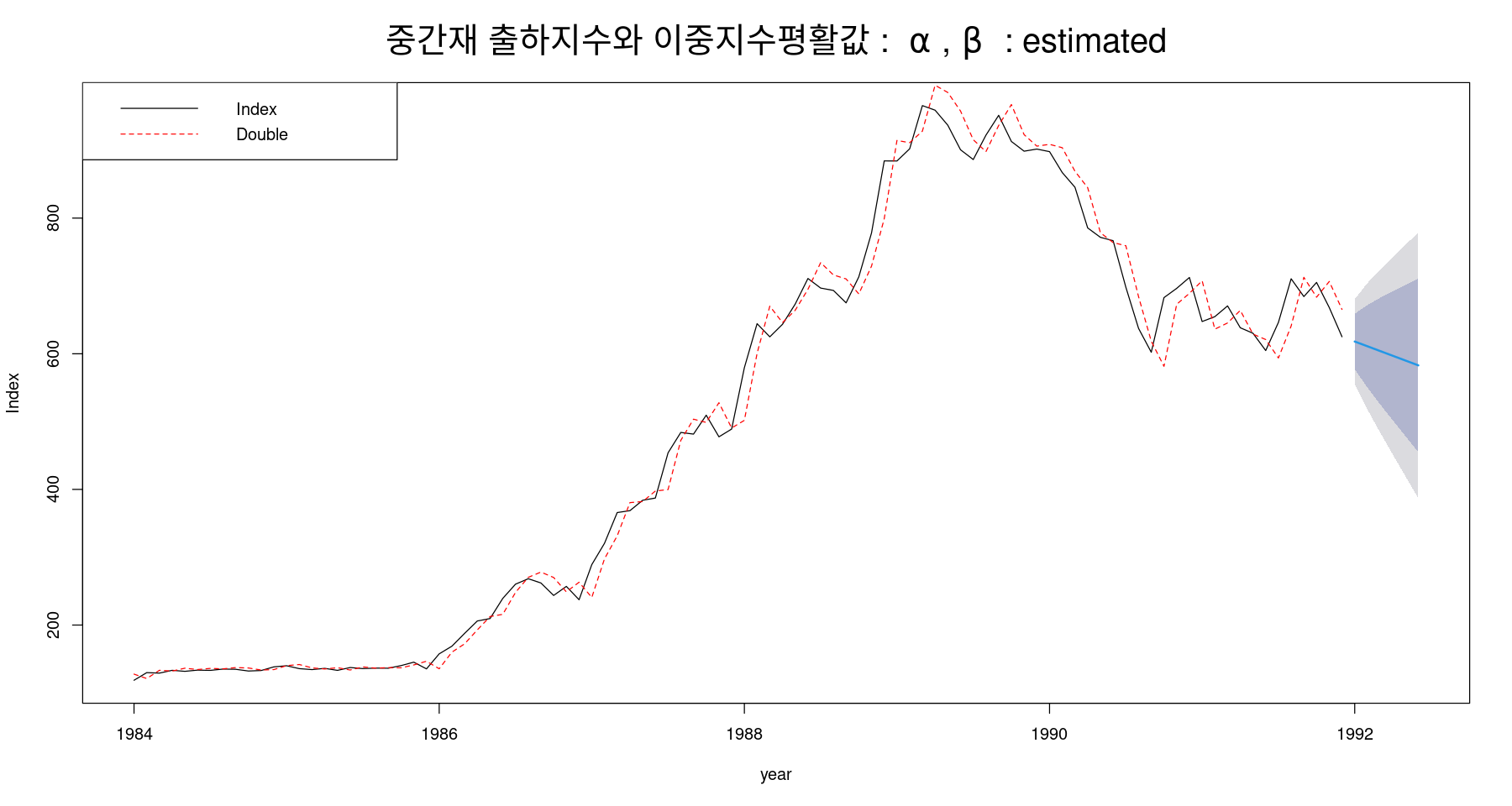

plot(resid(fit5), main=expression("Residual Plot : "~alpha~","~beta~ " : estimated"),
 cex.main=2)
abline(h=0)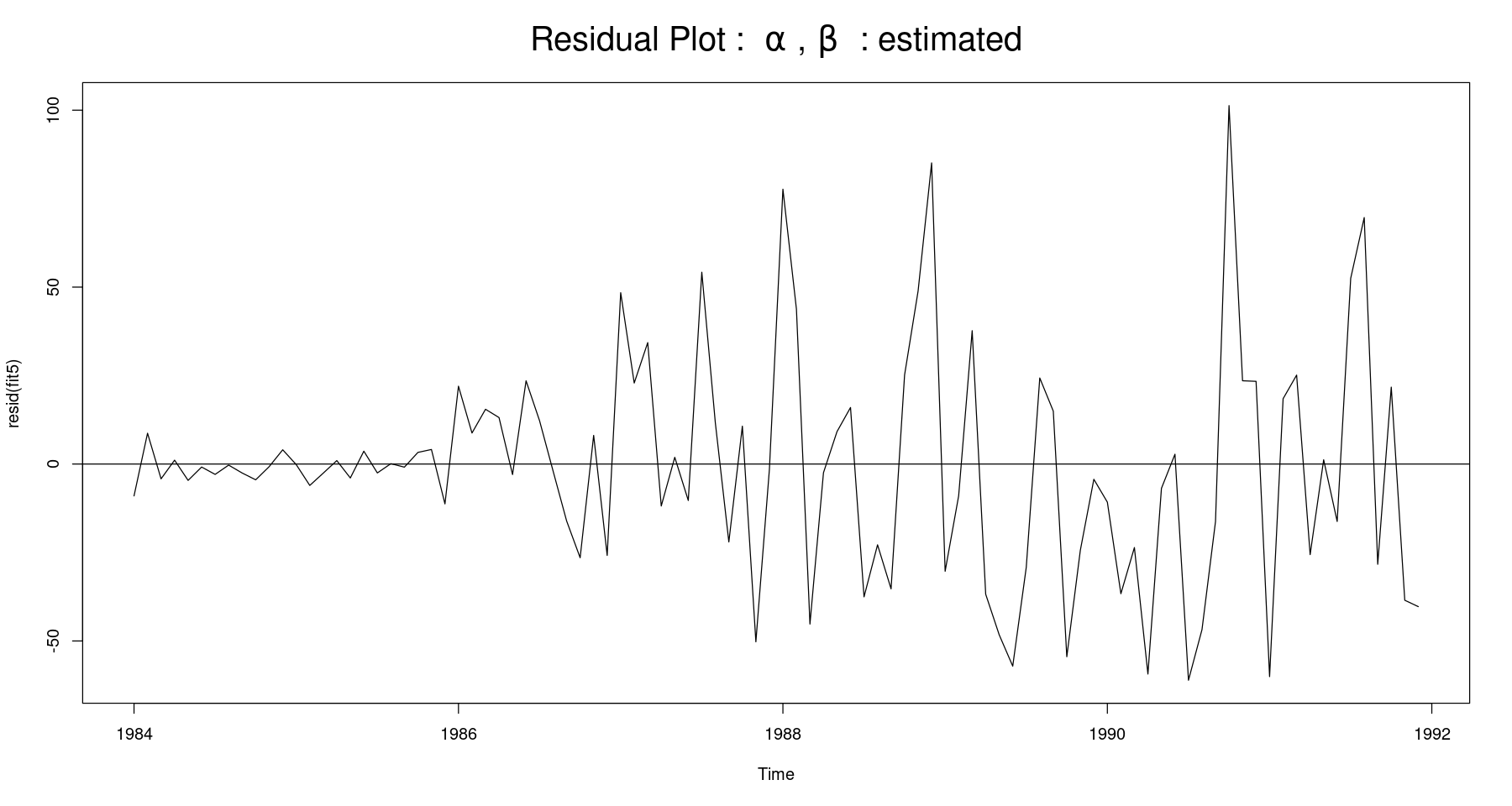

dwtest(lm(fit5$residuals~1), alternative = "two.sided")

    Durbin-Watson test

data:  lm(fit5$residuals ~ 1)
DW = 1.658, p-value = 0.09054
alternative hypothesis: true autocorrelation is not 0

계절지수평활

z <- scan("koreapass.txt")
pass <- ts(z, start=c(1981,1), frequency=12)

ts에 주기가 들어가 있어야 holtwinter에서 계절을 적합할 수 있다

plot.ts(pass)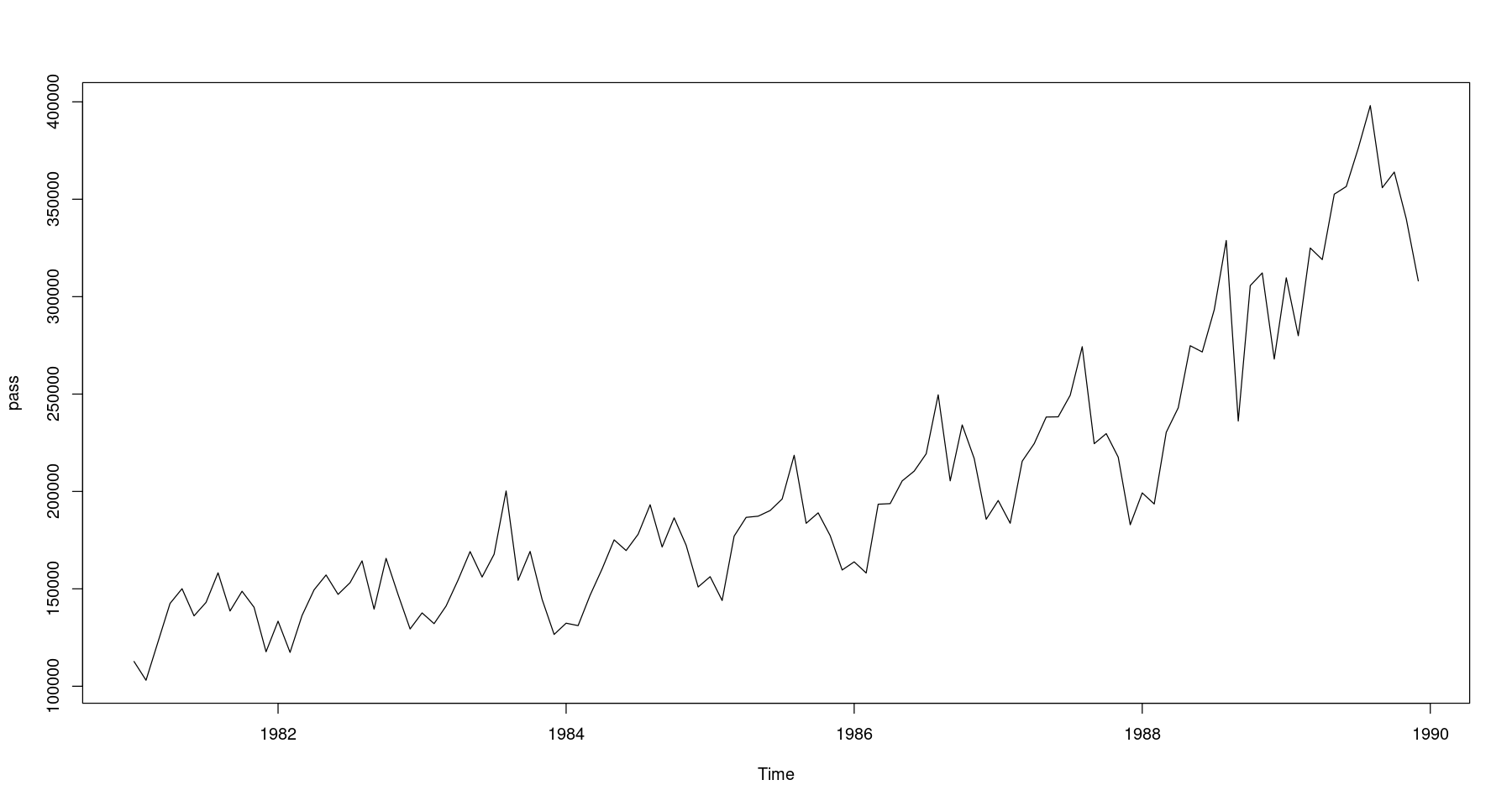

가법 모형? 승법 모형? 무엇을 쓸지 정해줘야 함

Holt Winters additive model

fit_hw <- HoltWinters(pass, seasonal="additive") #default는 additive
fit_hw
Holt-Winters exponential smoothing with trend and additive seasonal component.

Call:
HoltWinters(x = pass, seasonal = "additive")

Smoothing parameters:
 alpha: 0.4810767
 beta : 0.0383379
 gamma: 0.7345988

Coefficients:
          [,1]
a   347794.753
b     3363.251
s1  -12186.666
s2  -33643.322
s3    4855.643
s4    5000.713
s5   29085.909
s6   22953.006
s7   32200.195
s8   49687.643
s9  -11655.430
s10  10218.813
s11  -4226.391
s12 -38683.394
head(fit_hw$fitted)
A Time Series: 6 × 4
xhat level trend season
Jan 1982 128208.0 135375.1 769.6180 -7936.701
Feb 1982 114877.0 138637.6 865.1923 -24625.868
Mar 1982 135627.2 140706.0 911.3201 -5990.160
Apr 1982 149303.2 141945.3 923.8952 6433.924
May 1982 156969.9 142952.4 927.0829 13090.465
Jun 1982 147259.4 143945.4 929.6108 2384.382 
135375.1+769.6180-7936.701
128208.017

xhat = level + trend + season

- 계절지수평활 예측

\[\hat{Z}_n(k) = \hat{T}_n + \hat{\beta}_{1,n}k + \hat{S}_{n+k-s}, k=1,2,\dots, s\]

plot(fit_hw, lwd=2)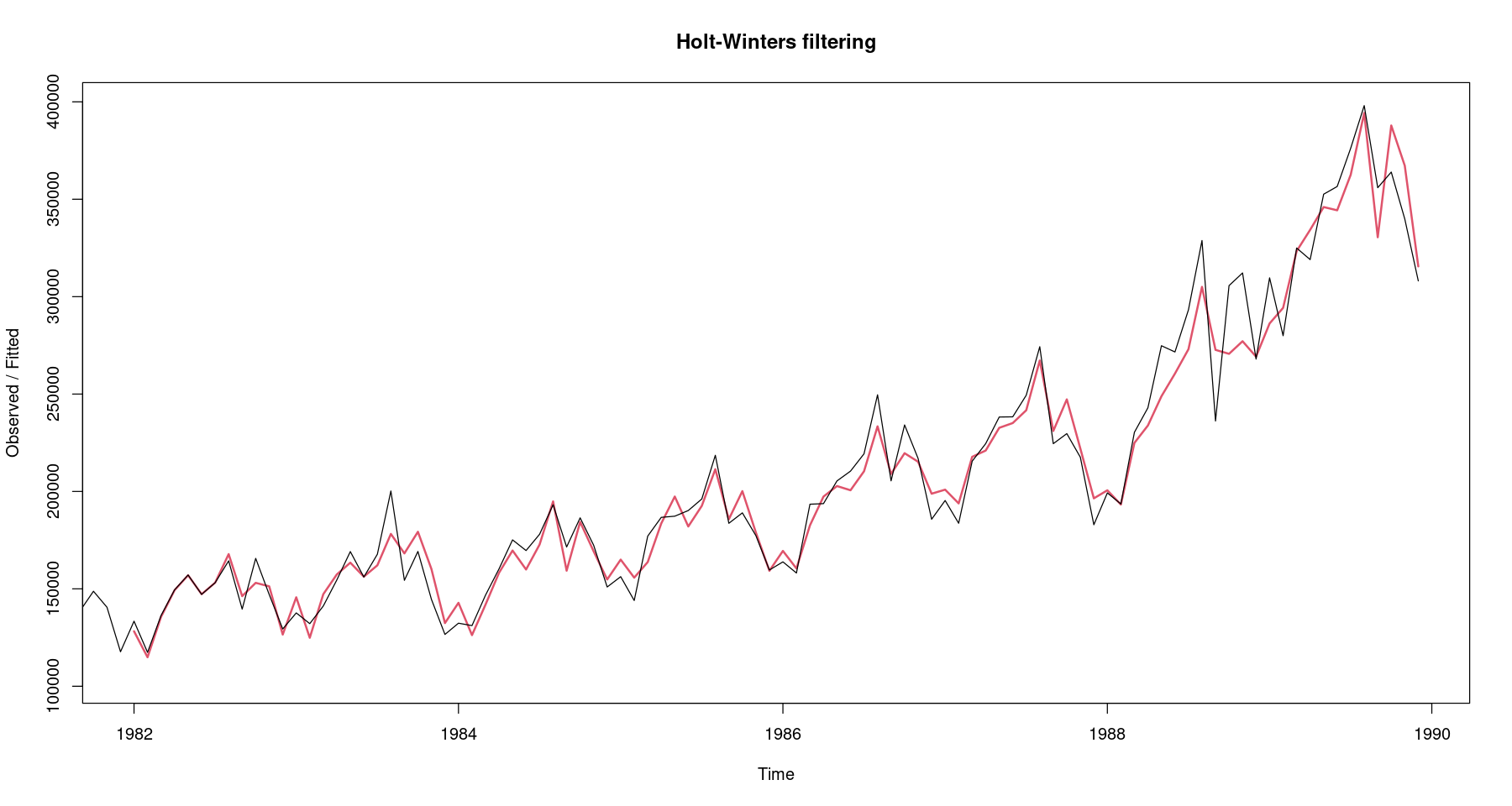

predict(fit_hw, n.ahead=12, prediction.interval = T, level=0.95)
A Time Series: 12 × 3
fit upr lwr
Jan 1990 338971.3 362386.4 315556.2
Feb 1990 320877.9 347051.8 294704.1
Mar 1990 362740.1 391587.4 333892.9
Apr 1990 366248.5 397711.4 334785.5
May 1990 393696.9 427736.7 359657.1
Jun 1990 390927.3 427518.3 354336.2
Jul 1990 403537.7 442664.2 364411.2
Aug 1990 424388.4 466041.9 382734.9
Sep 1990 366408.6 410586.3 322230.9
Oct 1990 391646.1 438349.7 344942.5
Nov 1990 380564.1 429798.8 331329.4
Dec 1990 349470.4 401244.2 297696.5 
fit6= hw(pass,
 alpha = fit_hw$alpha,
 beta = fit_hw$beta,
 gamma = fit_hw$gamma,
 seasonal="additive",
 initial="simple",
 h=12)
fit6$model
Holt-Winters' additive method 

Call:
 hw(y = pass, h = 12, seasonal = "additive", initial = "simple",  

 Call:
     alpha = fit_hw$alpha, beta = fit_hw$beta, gamma = fit_hw$gamma) 

  Smoothing parameters:
    alpha = 0.4811 
    beta  = 0.0383 
    gamma = 0.7346 

  Initial states:
    l = 134510.75 
    b = 874.0694 
    s = -16817.75 6028.25 14250.25 4115.25 23712.25 8522.25
           1617.25 15553.25 7985.25 -11710.75 -31440.75 -21814.75

  sigma:  12483.69
fit6
         Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
Jan 1990       339962.9 323964.4 355961.4 315495.3 364430.4
Feb 1990       307759.0 289731.1 325786.9 280187.7 335330.3
Mar 1990       354907.1 334791.7 375022.5 324143.3 385670.9
Apr 1990       353308.1 331046.6 375569.6 319262.1 387354.2
May 1990       391666.8 367200.6 416133.1 354249.0 429084.7
Jun 1990       393291.1 366562.0 420020.2 352412.5 434169.7
Jul 1990       408050.5 379001.1 437099.9 363623.2 452477.8
Aug 1990       428126.3 396699.7 459552.8 380063.5 476189.1
Sep 1990       374195.2 340335.6 408054.7 322411.4 425978.9
Oct 1990       381277.1 344929.5 417624.7 325688.2 436866.0
Nov 1990       373366.6 334476.8 412256.5 313889.7 432843.5
Dec 1990       347593.0 306107.7 389078.3 284146.7 411039.3
plot(fit6, ylab="passenger", xlab="year", lty=1, col="blue",
 main="Winters 가법계절지수평활된 자료의 시계열 그림",
 cex.main=2)
lines(fit6$fitted, lwd=3, col='red', lty=2)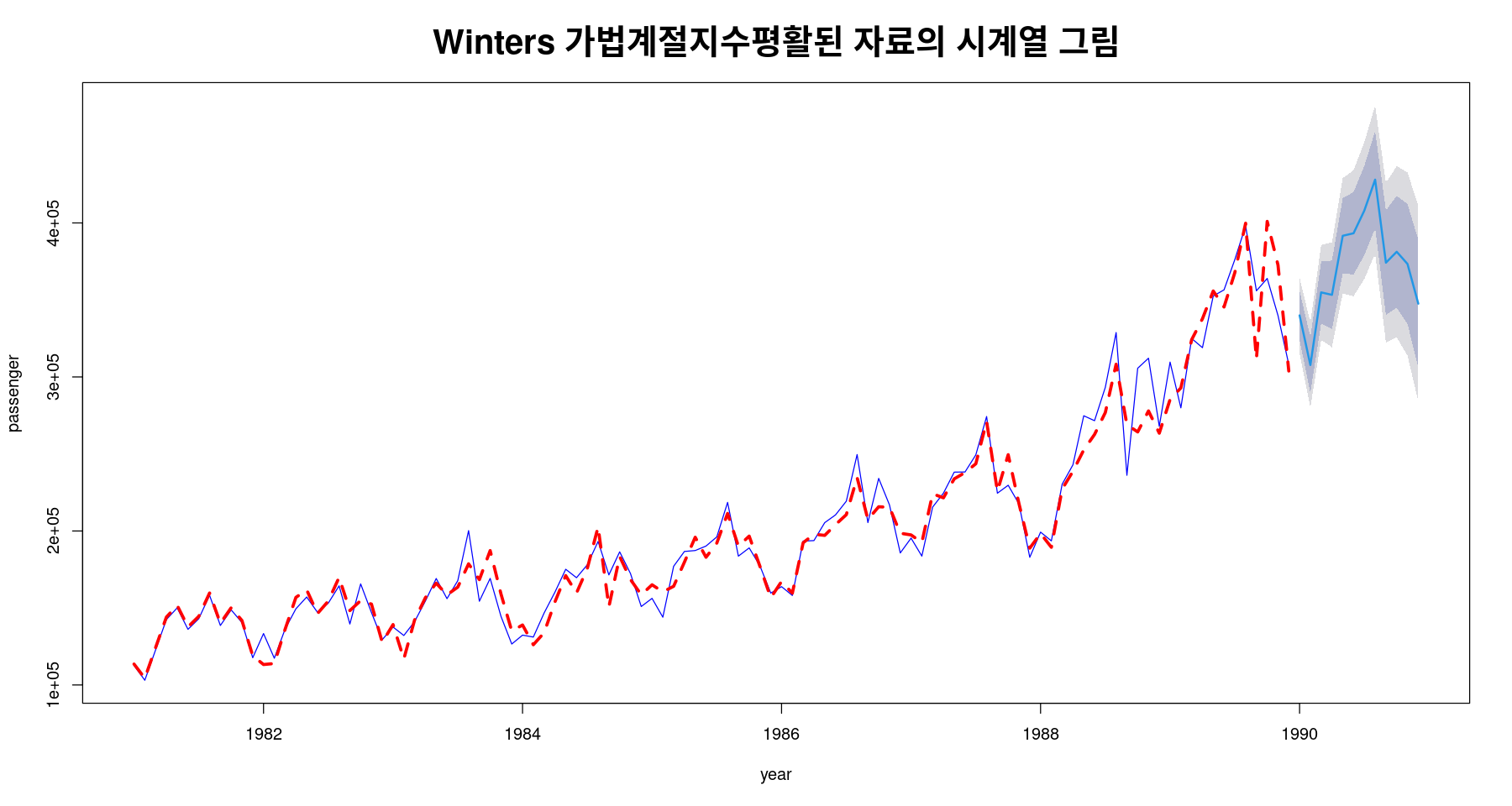

ts.plot(fit6$residual, ylab="residual",
 main="가법모형의 잔차 그림",
 cex.main=2); abline(h=0)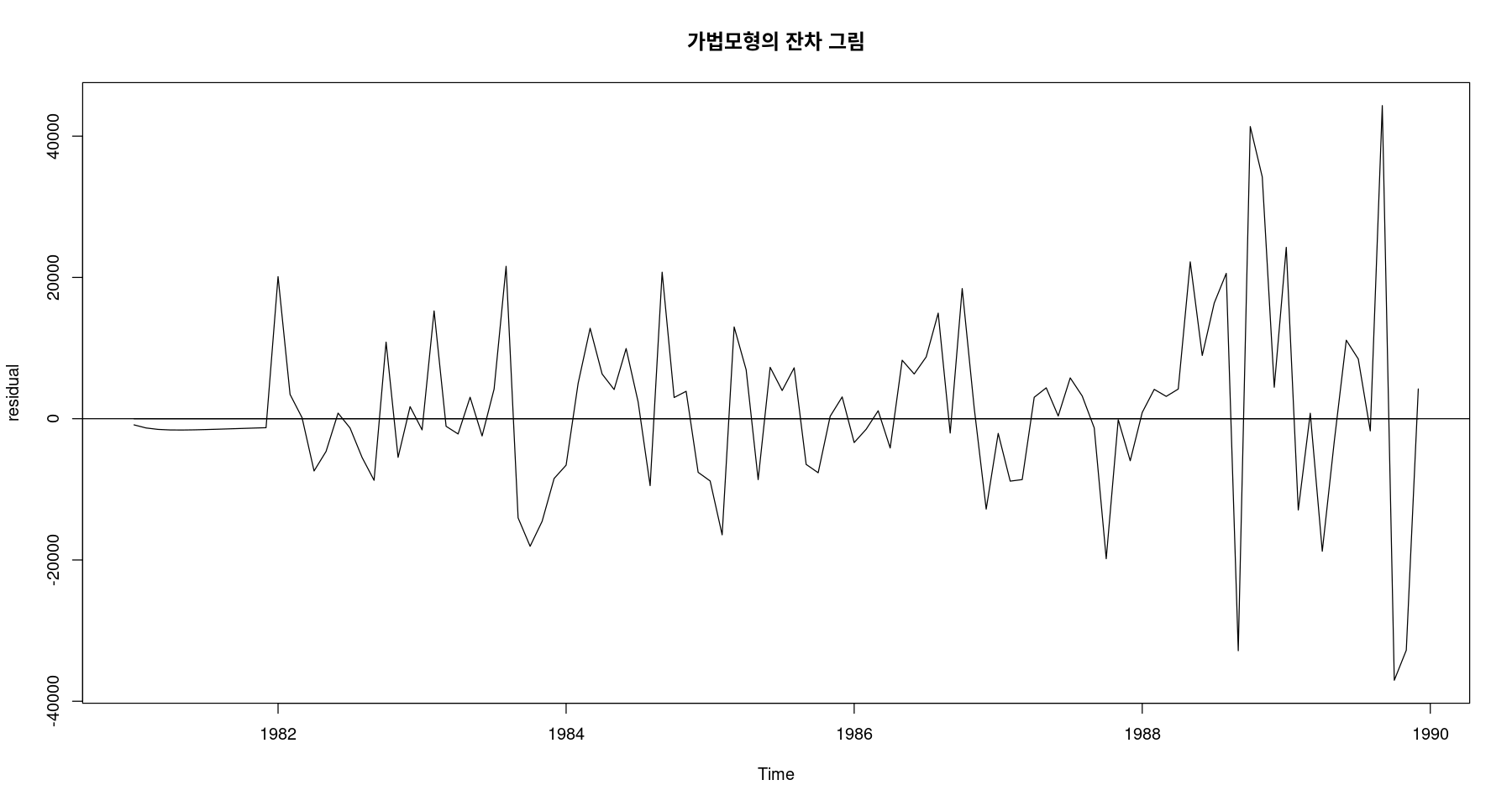

dwtest(lm(fit6$residual~1), alternative = 'two.sided')

    Durbin-Watson test

data:  lm(fit6$residual ~ 1)
DW = 1.9794, p-value = 0.9139
alternative hypothesis: true autocorrelation is not 0

Holt Winters multiplicative model

fit_hw_m <- HoltWinters(pass, seasonal="multiplicative")
fit_hw_m
Holt-Winters exponential smoothing with trend and multiplicative seasonal component.

Call:
HoltWinters(x = pass, seasonal = "multiplicative")

Smoothing parameters:
 alpha: 0.5623303
 beta : 0.03452066
 gamma: 0.3506508

Coefficients:
            [,1]
a   3.560417e+05
b   3.517556e+03
s1  9.199511e-01
s2  8.489190e-01
s3  9.796617e-01
s4  1.016528e+00
s5  1.095078e+00
s6  1.060795e+00
s7  1.089621e+00
s8  1.178393e+00
s9  9.706046e-01
s10 1.065056e+00
s11 9.983082e-01
s12 8.552947e-01
predict(fit_hw_m, n.ahead=12, prediction.interval = T, level=0.95)
A Time Series: 12 × 3
fit upr lwr
Jan 1990 330777.0 346829.6 314724.3
Feb 1990 308222.8 328288.3 288157.4
Mar 1990 359138.5 385415.3 332861.7
Apr 1990 376229.1 406856.5 345601.8
May 1990 409153.3 445160.0 373146.6
Jun 1990 400075.7 438217.8 361933.6
Jul 1990 414780.3 456969.6 372591.0
Aug 1990 452717.7 501167.0 404268.5
Sep 1990 376303.1 419627.5 332978.8
Oct 1990 416668.2 466954.3 366382.1
Nov 1990 394067.0 444265.0 343869.1
Dec 1990 340623.2 383998.5 297247.9

- 예측

\[\hat{Z}(l) = \hat{T}_n(l) \times \hat{S}_{n+l-ks}, k= \left[ \frac{l}{s} \right] +1\]

(135375.1+769.6180)*0.9434021
128439.212865108

xhat = (level+trend)*season

fit_hw_m$fitted
A Time Series: 96 × 4
xhat level trend season
Jan 1982 128439.2 135375.1 769.6180 0.9434021
Feb 1982 115639.6 139095.7 871.4889 0.8261910
Mar 1982 136017.4 141150.4 912.3332 0.9574463
Apr 1982 149518.1 142234.0 918.2449 1.0444694
May 1982 157061.6 143129.5 917.4625 1.0903497
Jun 1982 147301.4 144070.4 918.2707 1.0159511
Jul 1982 153718.4 144910.4 915.5686 1.0541223
Aug 1982 168929.0 145526.0 905.2115 1.1536408
Sep 1982 145356.8 144200.2 828.1961 1.0022647
Oct 1982 152328.4 141789.5 716.3873 1.0689275
Nov 1982 151308.0 149505.0 958.0018 1.0056162
Dec 1982 124771.8 148084.2 875.8840 0.8376189
Jan 1983 145221.4 152064.5 983.0515 0.9488645
Feb 1983 123699.8 148553.4 827.9091 0.8280811
Mar 1983 149535.4 155104.7 1025.4840 0.9577609
Apr 1983 158835.4 151223.3 856.0960 1.0444242
May 1983 164154.8 149769.4 776.3532 1.0903980
Jun 1983 156407.8 153110.0 864.8720 1.0158013
Jul 1983 162915.9 153780.1 858.1482 1.0535292
Aug 1983 181695.3 157217.9 947.2020 1.1487696
Sep 1983 167826.2 167237.0 1260.3691 0.9960164
Oct 1983 175269.4 160900.9 998.1329 1.0825849
Nov 1983 159827.9 158745.8 889.2831 1.0012074
Dec 1983 127751.9 151079.0 593.9197 0.8422859
Jan 1984 142532.5 150897.2 567.1406 0.9410302
Feb 1984 121903.3 145386.7 357.3392 0.8364204
Mar 1984 144778.3 151942.5 571.3136 0.9492795
Apr 1984 160473.4 153685.4 611.7569 1.0400279
May 1984 169547.0 154175.9 607.5694 1.0953819
Jun 1984 160803.2 157650.1 706.5277 1.0154502
Jul 1984 173694.6 163258.5 875.7438 1.0582471
Aug 1984 195138.7 166434.3 955.1427 1.1657766
Sep 1984 164547.1 166439.3 922.3449 0.9831827
Oct 1984 185610.3 171326.4 1059.2090 1.0767162
Nov 1984 171413.6 172820.4 1074.2210 0.9857326
Dec 1984 147645.7 174444.8 1093.2124 0.8411041
Jan 1985 166446.4 177748.5 1169.5180 0.9302943
Feb 1985 146908.1 172748.6 956.5467 0.8457327
Mar 1985 164250.1 171776.8 889.9809 0.9512544
Apr 1985 188619.2 180247.0 1151.6551 1.0398045
May 1985 199768.4 180357.0 1115.6953 1.1008179
Jun 1985 180180.9 175101.4 895.7550 1.0237712
Jul 1985 193953.7 181503.7 1085.8446 1.0622383
Aug 1985 215179.5 183742.8 1125.6531 1.1639604
Sep 1985 185692.7 186501.6 1182.0312 0.9893921
Oct 1985 202200.9 186523.2 1141.9731 1.0774556
Nov 1985 179243.3 180777.1 904.1926 0.9865810
Dec 1985 153140.0 180587.9 866.4476 0.8439588
Jan 1986 172106.7 185806.6 1016.6913 0.9212270
Feb 1986 153977.5 181780.9 842.6228 0.8431417
Mar 1986 179279.4 185389.7 938.1127 0.9621723
Apr 1986 203305.2 194607.3 1223.9257 1.0381655
May 1986 208927.8 190651.8 1045.1284 1.0898863
Jun 1986 197018.2 189880.8 982.4368 1.0322479
Jul 1986 212180.6 198172.2 1234.7474 1.0640578
Aug 1986 238655.1 203183.2 1365.1045 1.1667422
Sep 1986 208779.2 209829.1 1547.4027 0.9877122
Oct 1986 224934.7 209476.6 1481.8151 1.0662514
Nov 1986 214191.6 215814.8 1649.4602 0.9849507
Dec 1986 187470.3 219018.0 1703.0961 0.8493540
Jan 1987 202258.4 219564.9 1663.1842 0.9142529
Feb 1987 184970.6 216976.5 1516.4157 0.8465751
Mar 1987 213274.2 217628.3 1486.5694 0.9733442
Apr 1987 228708.4 220414.6 1531.4390 1.0304682
May 1987 240375.6 219675.2 1453.0466 1.0870415
Jun 1987 230858.4 220003.3 1414.2138 1.0426382
Jul 1987 242751.4 225433.2 1552.8376 1.0694549
Aug 1987 272726.7 230482.5 1673.5374 1.1747561
Sep 1987 231155.7 232912.5 1699.6504 0.9852673
Oct 1987 249317.1 230829.5 1569.0702 1.0727996
Nov 1987 220386.3 222107.5 1213.8155 0.9868577
Dec 1987 189030.6 221719.9 1158.5349 0.8481333
Jan 1988 199905.9 218812.4 1018.1716 0.9093637
Feb 1988 186408.5 219426.2 1004.2127 0.8456572
Mar 1988 220678.5 225189.2 1168.4887 0.9749107
Apr 1988 239733.3 231942.0 1361.2624 1.0275610
May 1988 256712.8 235065.2 1422.0871 1.0855245
Jun 1988 259416.0 245858.0 1745.5700 1.0477070
Jul 1988 275036.2 254142.5 1971.2982 1.0738826
Aug 1988 315076.2 265667.0 2301.0825 1.1757973
Sep 1988 271768.2 274543.1 2528.0540 0.9808608
Oct 1988 273789.7 256655.7 1823.2999 1.0592337
Nov 1988 273615.5 275399.5 2407.4071 0.9849124
Dec 1988 255666.9 299816.0 3167.1744 0.8438321
Jan 1989 285956.7 311166.6 3449.6732 0.9089063
Feb 1989 283426.4 329277.5 3955.7888 0.8505344
Mar 1989 328551.3 330930.3 3876.2862 0.9813167
Apr 1989 346538.9 332750.4 3805.3046 1.0296631
May 1989 356260.4 321526.7 3286.4962 1.0968162
Jun 1989 344118.9 322937.6 3221.7479 1.0550639
Jul 1989 364618.5 332782.7 3450.3919 1.0844217
Aug 1989 409371.2 342246.0 3657.9609 1.1834823
Sep 1989 330102.0 340538.5 3472.7404 0.9595674
Oct 1989 391103.1 359147.7 3995.2609 1.0769949
Nov 1989 354111.2 348968.1 3505.9370 1.0046446
Dec 1989 295543.2 344512.4 3231.0940 0.8498887 
fit7= hw(pass,
 alpha = fit_hw_m$alpha,
 beta = fit_hw_m$beta,
 gamma = fit_hw_m$gamma,
 seasonal="multiplicative",
 initial="simple",
 h=12)
fit7$model
Holt-Winters' multiplicative method 

Call:
 hw(y = pass, h = 12, seasonal = "multiplicative", initial = "simple",  

 Call:
     alpha = fit_hw_m$alpha, beta = fit_hw_m$beta, gamma = fit_hw_m$gamma) 

  Smoothing parameters:
    alpha = 0.5623 
    beta  = 0.0345 
    gamma = 0.3507 

  Initial states:
    l = 134510.75 
    b = 874.0694 
    s = 0.875 1.0448 1.1059 1.0306 1.1763 1.0634
           1.012 1.1156 1.0594 0.9129 0.7663 0.8378

  sigma:  0.053
plot(fit7, ylab="passenger", xlab="year", lty=1, col="blue",
 main="Winters 승법계절지수평활된 자료의 시계열 그림",
 cex.main=2)
lines(fit7$fitted, col="red", lty=2)
legend("topleft", lty=1:2, col=c("blue","red"), c("Pass", "Multiplicative"))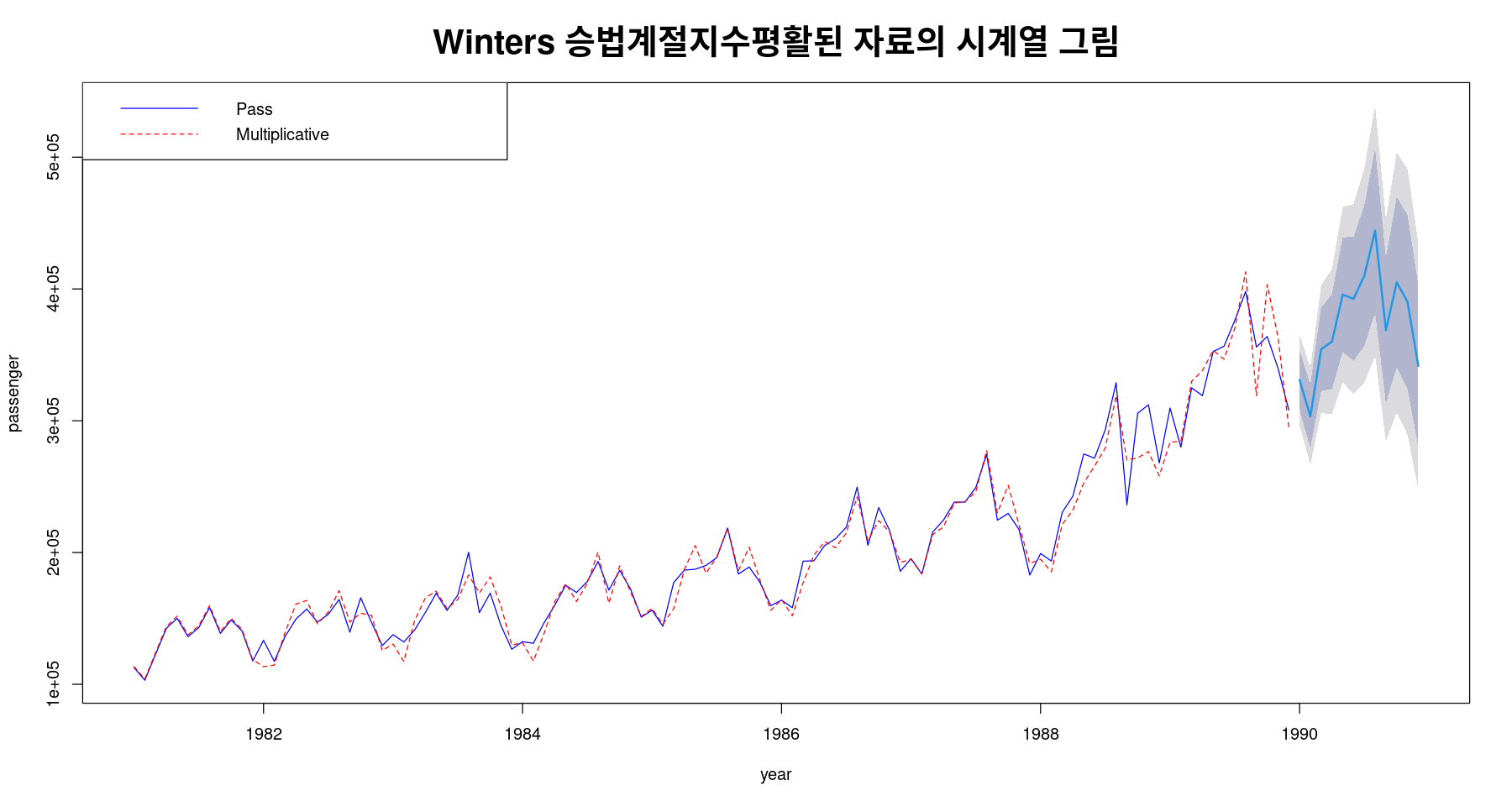

ts.plot(fit7$residual, ylab="residual",
 main="승법모형의 잔차 그림",
 cex.main=2); abline(h=0)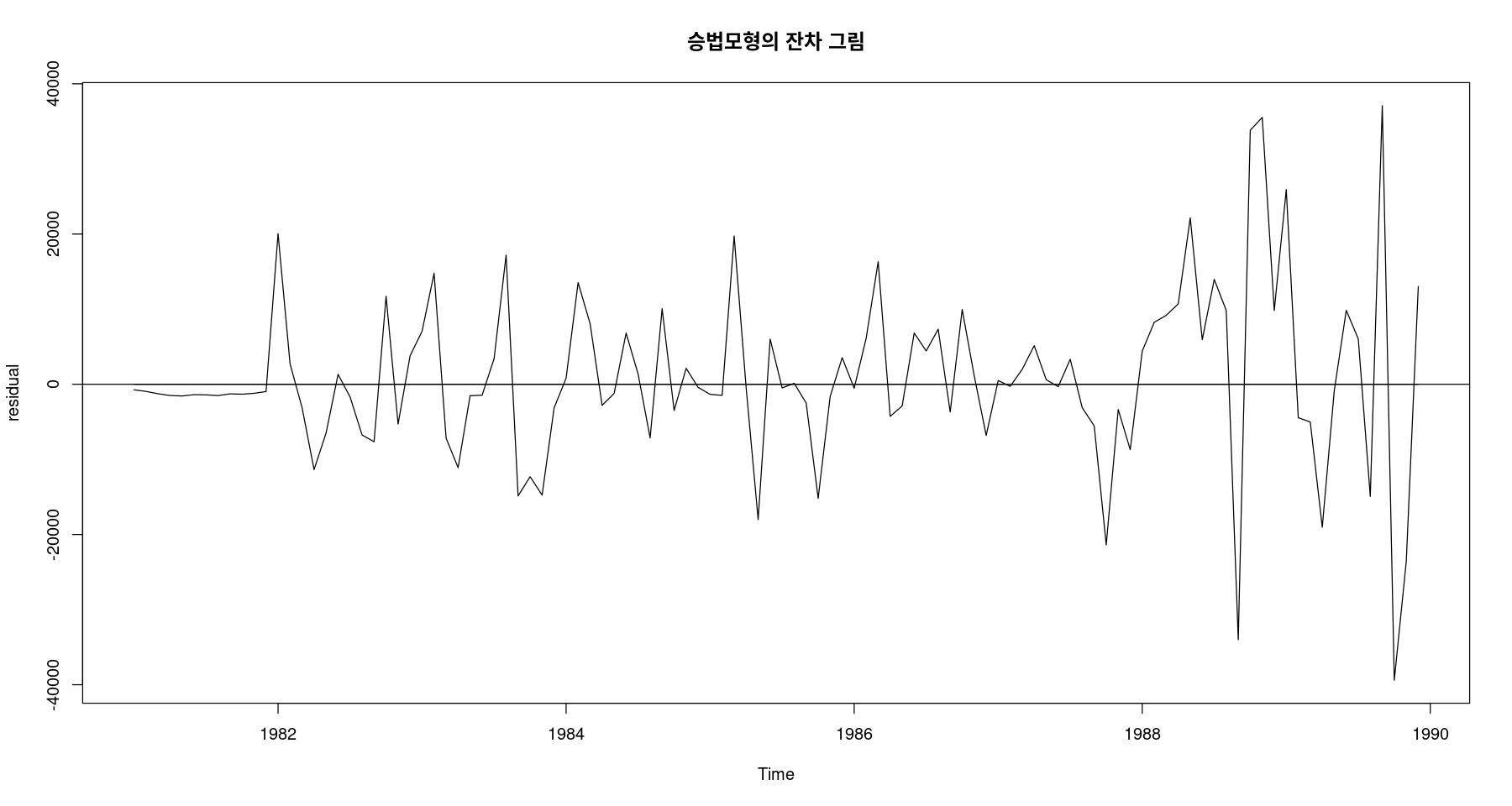

dwtest(lm(fit7$residual~1), alternative = 'two.sided')

    Durbin-Watson test

data:  lm(fit7$residual ~ 1)
DW = 1.9744, p-value = 0.8931
alternative hypothesis: true autocorrelation is not 0
fit_hw$SSE
13764737658.0239 
fit_hw_m$SSE
12633778874.3409

가법과 승법 모형의 SSE를 비교해서 SSE값이 더 작은 모형을 선택해 주자.

함수 정리

단순지수평활: HoltWinters(beta=gamma=FALSE), ses: 추세도 없고 계절성분도 없어보일 때 사용

이중지수평활: HoltWinters(gamma=FALSE), holt: 추세가 있을 때 사용

계절지수평활: HoltWinters(), hw: 계절 성분 있을 때 사용

위의 함수를 사용하기 전에 가장 먼저 시도표를 보자!